CF1198E Rectangle Painting 2

There is a square grid of size $ n \times n $ . Some cells are colored in black, all others are colored in white. In one operation you can select some rectangle and color all its cells in white. It costs $ \min(h, w) $ to color a rectangle of size $ h \times w $ . You are to make all cells white for minimum total cost. The square is large, so we give it to you in a compressed way. The set of black cells is the union of $ m $ rectangles.

The first line contains two integers $ n $ and $ m $ ( $ 1 \le n \le 10^{9} $ , $ 0 \le m \le 50 $ ) — the size of the square grid and the number of black rectangles. Each of the next $ m $ lines contains 4 integers $ x_{i1} $ $ y_{i1} $ $ x_{i2} $ $ y_{i2} $ ( $ 1 \le x_{i1} \le x_{i2} \le n $ , $ 1 \le y_{i1} \le y_{i2} \le n $ ) — the coordinates of the bottom-left and the top-right corner cells of the $ i $ -th black rectangle. The rectangles may intersect.

Print a single integer — the minimum total cost of painting the whole square in white.

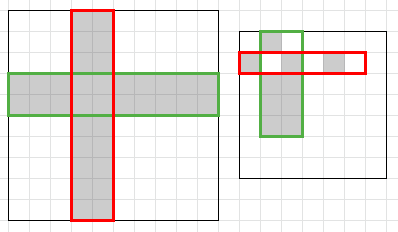
The examples and some of optimal solutions are shown on the pictures below.