CF1198E Rectangle Painting 2
题目描述
有一个$n*n$的网格,网格中有一些点是黑的,其他点都是白的。你每次可以花费$\min(h,w)$的代价把一个$h*w$的矩形区域变白。求把所有黑格变白的最小代价。
输入格式
第一行2个整数$n$,$m$($1\le n \le 10^9,0\le m\le 50$),分别代表正方形网格的大小和**黑色矩形**的数量。
接下来$m$行,每行$4$个整数$x_{i1},y_{i1},x_{i2},y_{i2}$($1\le x_{i1}\le x_{i2}\le n,1\le y_{i1}\le y_{i2}\le n$),分别代表黑色矩形左下角的格子和右上角的格子。(显然,黑色矩形里的格子都是黑的。)
黑色矩形可能相交。
输出格式
一个整数:把所有格子变白的最小代价。
说明/提示
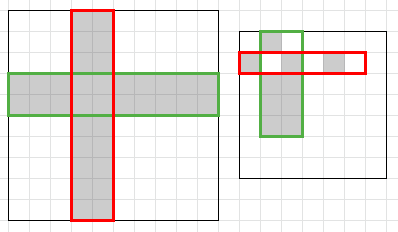
The examples and some of optimal solutions are shown on the pictures below.