CF1199B Water Lily

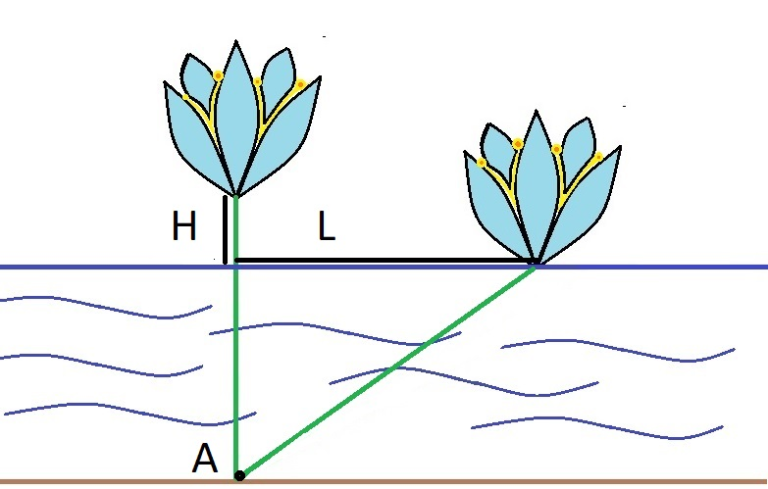While sailing on a boat, Inessa noticed a beautiful water lily flower above the lake's surface. She came closer and it turned out that the lily was exactly $ H $ centimeters above the water surface. Inessa grabbed the flower and sailed the distance of $ L $ centimeters. Exactly at this point the flower touched the water surface. Suppose that the lily grows at some point $ A $ on the lake bottom, and its stem is always a straight segment with one endpoint at point $ A $ . Also suppose that initially the flower was exactly above the point $ A $ , i.e. its stem was vertical. Can you determine the depth of the lake at point $ A $ ?

The only line contains two integers $ H $ and $ L $ ( $ 1 \le H < L \le 10^{6} $ ).

Print a single number — the depth of the lake at point $ A $ . The absolute or relative error should not exceed $ 10^{-6} $ . Formally, let your answer be $ A $ , and the jury's answer be $ B $ . Your answer is accepted if and only if $ \frac{|A - B|}{\max{(1, |B|)}} \le 10^{-6} $ .