CF119B Before Exam

Vasya is about to take his first university exam in about several minutes. And it's not just some ordinary exam, it's on mathematical analysis. Of course, right now Vasya can only think of one thing: what the result of his talk with the examiner will be... To prepare for the exam, one has to study proofs of $ n $ theorems. It is known that there will be $ k $ examination cards on the exam and each card contains 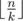 distinct theorems. Besides, no theorem is mentioned in more than one card (that is, 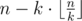 theorems won't be mentioned in any card). During the exam several students may get the same card. We do not know the exact way theorems are distributed by cards, however the students that took the exam before Vasya told him what theorems their cards contained. Vasya evaluates his level of proficiency in the $ i $ -th theorem by some number $ a_{i} $ . The level of proficiency in some card is the average of the levels of proficiency in the theorems that are included in the card. Now Vasya wants to know the minimally and maximally possible levels of his proficiency in the card he gets on the exam. Vasya wants to determine it by the data he has collected from other students. Unfortunately, Vasya has no time left to do the math and he asked you to help him.

The first line contains two integers $ n $ and $ k $ ( $ 1

Print two real numbers, representing Vasya's minimum and maximum proficiency in the card he will get on the exam. The absolute or relative error should not exceed $ 10^{-6} $ .

Let's analyze the first sample. Vasya's proficiency in the cards whose content he already knows equals $ 6 $ and $ 15.5 $ correspondingly. The three theorems that are left are only enough to make one exam card. If we consider all possible variants of theorems included in the card we can see that in the best case scenario Vasya gets the card that contains theorems $ 4 $ and $ 7 $ (his proficiency would equal $ 15.5 $ ) and in the worst case scenario he gets theorems $ 3 $ and $ 5 $ (his proficiency would equal $ 5 $ ). The $ ⌊\ x⌋ $ operation denotes taking integer part of real number $ x $ (rounding down).