CF1200F Graph Traveler

Gildong 正在用一台有趣的机器 Graph Traveler 进行实验。在 Graph Traveler 中，有一个有向图，包含 $n$ 个顶点，编号从 $1$ 到 $n$。第 $i$ 个顶点有 $m_i$ 条有向边，分别标记为 $e_i[0]$、$e_i[1]$、$\ldots$、$e_i[m_i-1]$，每条边表示该边的目标顶点。该图可以有重边和自环。第 $i$ 个顶点上还写有一个整数 $k_i$。 在这个图上的一次旅行按如下方式进行： 1. Gildong 选择一个顶点作为起点，并选择一个整数作为起始值。将变量 $c$ 设为该整数。 2. 每当到达顶点 $i$，或者刚开始在某个顶点 $i$ 开始旅行时，将 $k_i$ 加到 $c$ 上。 3. 下一个顶点为 $e_i[x]$，其中 $x$ 是满足 $0 \le x \le m_i-1$ 且 $x \equiv c \pmod{m_i}$ 的整数。前往下一个顶点并回到第 2 步。 显然，这样的旅行永远不会结束，因为第 2 步和第 3 步会无限循环。 例如，假设 Gildong 从顶点 $1$ 开始，$c=5$，且 $m_1=2$，$e_1[0]=1$，$e_1[1]=2$，$k_1=-3$。刚开始在顶点 $1$ 时，$c$ 变为 $2$。唯一满足条件的 $x$（$0 \le x \le 1$ 且 $x \equiv c \pmod{m_i}$）是 $0$，所以 Gildong 前往顶点 $e_1[0]=1$。再次到达顶点 $1$ 后，$c$ 变为 $-1$。唯一满足条件的 $x$ 是 $1$，所以他前往顶点 $e_1[1]=2$，以此类推。 由于 Gildong 非常好奇，他会向你提出 $q$ 个询问。他想知道，如果从某个顶点以某个 $c$ 的初始值开始旅行，将会有多少个不同的顶点被无限次访问。注意，不要统计那些只会被访问有限次的顶点。

输入的第一行包含一个整数 $n$（$1 \le n \le 1000$），表示图中顶点的数量。 第二行包含 $n$ 个整数，第 $i$ 个整数为 $k_i$（$-10^9 \le k_i \le 10^9$），表示第 $i$ 个顶点上的整数。 接下来的 $2 \cdot n$ 行描述每个顶点的边。第 $(2 \cdot i + 1)$ 行包含一个整数 $m_i$（$1 \le m_i \le 10$），表示第 $i$ 个顶点的出边数量。第 $(2 \cdot i + 2)$ 行包含 $m_i$ 个整数 $e_i[0]$、$e_i[1]$、$\ldots$、$e_i[m_i-1]$，每个整数的取值范围为 $1$ 到 $n$。 接下来一行包含一个整数 $q$（$1 \le q \le 10^5$），表示 Gildong 想要询问的次数。 接下来的 $q$ 行，每行包含两个整数 $x$ 和 $y$（$1 \le x \le n$，$-10^9 \le y \le 10^9$），表示起始顶点为 $x$，初始 $c$ 的值为 $y$。

对于每个询问，输出一个整数，表示如果 Gildong 从顶点 $x$ 以初始整数 $y$ 开始旅行，将会有多少个不同的顶点被无限次访问。

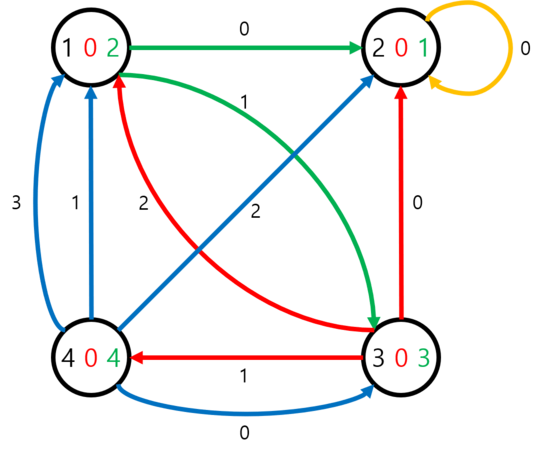
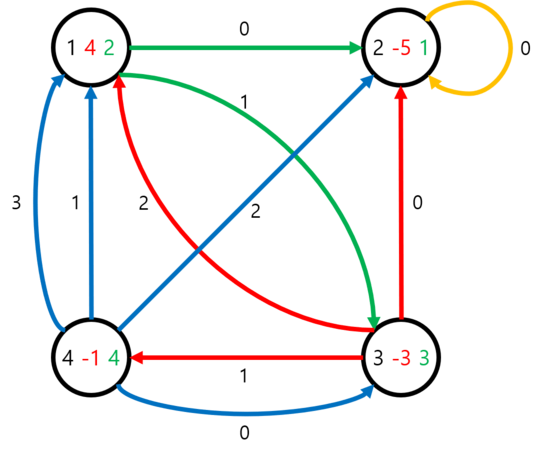
第一个样例可以用下图表示：  每个顶点上标记了三个整数：$i$、$k_i$ 和 $m_i$。出边用整数标记，表示该顶点的第几条边。 每个询问的旅行过程如下，描述为“顶点（加上 $k_i$ 后的 $c$ 值）”的序列： - $1(0) \to 2(0) \to 2(0) \to \ldots$ - $2(0) \to 2(0) \to \ldots$ - $3(-1) \to 1(-1) \to 3(-1) \to \ldots$ - $4(-2) \to 2(-2) \to 2(-2) \to \ldots$ - $1(1) \to 3(1) \to 4(1) \to 1(1) \to \ldots$ - $1(5) \to 3(5) \to 1(5) \to \ldots$ 第二个样例与第一个样例相同，只是顶点上的值非零，因此每个询问的答案也不同。  第二个样例的每个询问过程如下： - $1(4) \to 2(-1) \to 2(-6) \to \ldots$ - $2(-5) \to 2(-10) \to \ldots$ - $3(-4) \to 1(0) \to 2(-5) \to 2(-10) \to \ldots$ - $4(-3) \to 1(1) \to 3(-2) \to 4(-3) \to \ldots$ - $1(5) \to 3(2) \to 1(6) \to 2(1) \to 2(-4) \to \ldots$ - $1(9) \to 3(6) \to 2(1) \to 2(-4) \to \ldots$ 由 ChatGPT 4.1 翻译