CF1201D Treasure Hunting

有一个$n*m$的矩阵，行的标号从$1$到$n$，列的标号从$1$到$m$，矩阵中共有$k$个宝藏，第$i$个宝藏的位置为$(r_i,c_i)$。有$q$个安全的列，第$i$个安全的列的编号是$b_i$。 最初你站在矩阵的左下角（也就是$(1,1)$的位置），并且可以向左走（从$(r,c)$到$(r,c-1)$）和向右走（从$(r,c)$到$(r,c+1)$）。同时，你也可是向上走（从$(r,c)$到$(r+1,c)$），但是你必须在安全的列上。由于某些玄学原因，你不可以向下走。 你的任务是收集所有的宝藏，但是你的时间已经不多了，所以你必须走最快的路径。现在你要使用你的人脑大法来计算出最快的路径需要多少时间（经过有宝藏的格子时收集宝藏不消耗时间，只有移动消耗时间）。

无

无

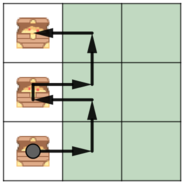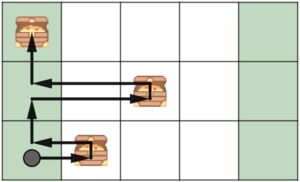In the first example you should use the second column to go up, collecting in each row treasures from the first column. In the second example, it is optimal to use the first column to go up. In the third example, it is optimal to collect the treasure at cell $ (1;6) $ , go up to row $ 2 $ at column $ 6 $ , then collect the treasure at cell $ (2;2) $ , go up to the top row at column $ 1 $ and collect the last treasure at cell $ (3;4) $ . That's a total of $ 15 $ moves.