CF1204C Anna, Svyatoslav and Maps

为了简洁，主角们被省略了。 给定一个有向无权图，无自环，共有 $n$ 个顶点，以及图中的一条路径（该路径不一定简单），路径由 $m$ 个顶点组成的序列 $p_1, p_2, \ldots, p_m$ 给出；对于每个 $1 \leq i < m$，都存在一条从 $p_i$ 到 $p_{i+1}$ 的有向边。 定义 $k$ 个顶点组成的序列 $v_1, v_2, \ldots, v_k$ 是“好”的，如果 $v$ 是 $p$ 的一个子序列，$v_1 = p_1$，$v_k = p_m$，并且 $p$ 是一条经过 $v_1, \ldots, v_k$（按顺序）的最短路径之一。 一个序列 $a$ 是序列 $b$ 的子序列，指的是 $a$ 可以通过从 $b$ 中删除若干（可能为零或全部）元素得到。显然，序列 $p$ 本身是“好”的，但你的任务是找到最短的“好”子序列。 如果有多组最短的“好”子序列，输出任意一组即可。

第一行包含一个整数 $n$（$2 \le n \le 100$），表示图中顶点的数量。 接下来的 $n$ 行描述图的邻接矩阵：第 $i$ 行的第 $j$ 个字符为 $1$ 表示存在一条从顶点 $i$ 到顶点 $j$ 的有向边，否则为 $0$。保证图中没有自环。 接下来一行包含一个整数 $m$（$2 \le m \le 10^6$），表示路径中顶点的数量。 下一行包含 $m$ 个整数 $p_1, p_2, \ldots, p_m$（$1 \le p_i \le n$），表示路径上的顶点序列。保证对于任意 $1 \leq i < m$，都存在一条从 $p_i$ 到 $p_{i+1}$ 的有向边。

第一行输出一个整数 $k$（$2 \leq k \leq m$），表示最短“好”子序列的长度。第二行输出 $k$ 个整数 $v_1, \ldots, v_k$（$1 \leq v_i \leq n$），表示该子序列中的顶点。如果有多组最短子序列，输出任意一组即可。任意两个相邻的数都应不同。

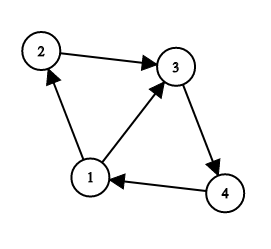
下面是第一个样例中的图示：  给定的路径经过顶点 $1, 2, 3, 4$。序列 $1-2-4$ 是“好”的，因为它是给定路径的子序列，首尾元素分别等于路径的首尾元素，并且经过顶点 $1, 2, 4$（按顺序）的最短路径是 $1-2-3-4$。注意，子序列 $1-4$ 和 $1-3-4$ 都不是“好”的，因为在这两种情况下，经过这些顶点的最短路径是 $1-3-4$。 在第三个样例中，图是完全图，因此任意两个相邻元素不同的顶点序列都对应一条长度相同的路径。 在第四个样例中，路径 $1-2-4$ 和 $1-3-4$ 都是经过顶点 $1$ 和 $4$ 的最短路径。 由 ChatGPT 4.1 翻译