CF1205A Almost Equal

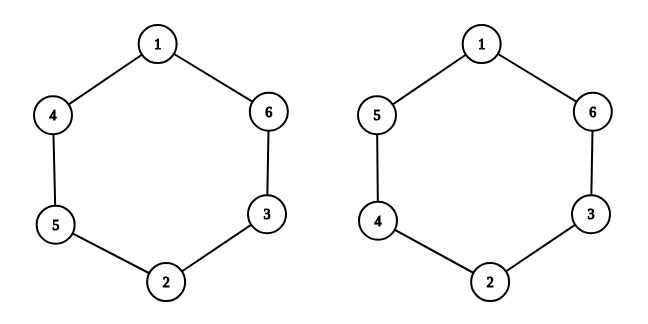
给定一个整数 $n$。你需要将 $1$ 到 $2n$ 的所有整数，每个数恰好使用一次，排列在一个圆环上，使得满足以下条件： 对于圆环上任意连续的 $n$ 个数，将它们的和写在黑板上。最终黑板上会写下 $2n$ 个数，要求这 $2n$ 个数中任意两个数的差不超过 $1$。 例如，当 $n=3$ 时，左图是一个合法的排列：$1+4+5=10$，$4+5+2=11$，$5+2+3=10$，$2+3+6=11$，$3+6+1=10$，$6+1+4=11$，任意两个数的差都不超过 $1$。右图是一个不合法的排列：例如，$5+1+6=12$，$3+2+4=9$，$9$ 和 $12$ 的差超过了 $1$。 

输入仅一行，包含一个整数 $n$（$1 \leq n \leq 10^5$）。

如果无解，第一行输出 "NO"。 如果有解，第一行输出 "YES"。第二行输出 $2n$ 个数，表示从 $1$ 到 $2n$ 的一个排列，按照它们在圆环上的顺序排列。每个数只能出现一次。如果有多种方案，可以输出任意一种。

样例中的排列即为第一个样例的解。 可以证明，第二个样例无解。 由 ChatGPT 4.1 翻译