CF1205C Palindromic Paths

这是一个交互题。 你有一个 $n \times n$ 的网格，其中 $n$ 是奇数。行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $n$。位于第 $x$ 行第 $y$ 列的格子记作 $(x, y)$。 每个格子中包含 $0$ 或 $1$。已知左上角格子为 $1$，右下角格子为 $0$。 你的目标是确定网格中所有格子的数值。为此，你可以进行如下询问： “$?$ $x_1$ $y_1$ $x_2$ $y_2$”，其中 $1 \le x_1 \le x_2 \le n$，$1 \le y_1 \le y_2 \le n$，并且 $x_1 + y_1 + 2 \le x_2 + y_2$。换句话说，你需要输出网格中两个不同的格子 $(x_1, y_1)$ 和 $(x_2, y_2)$，并且可以仅通过向右或向下移动从第一个格子走到第二个格子，且它们不是相邻的。 对于每次这样的询问，你会被告知是否存在一条从 $(x_1, y_1)$ 到 $(x_2, y_2)$ 仅向右或向下移动的路径，使得路径上经过的格子中的数字序列构成一个回文串。 例如，图中绿色的路径是回文路径，因此对于“$?$ $1$ $1$ $2$ $3$”和“$?$ $1$ $2$ $3$ $3$”的答案都是存在这样的路径。然而，对于“$?$ $1$ $1$ $3$ $1$”则不存在回文路径。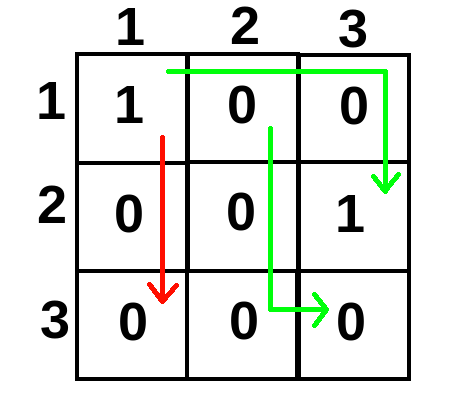  请通过不超过 $n^2$ 次询问，确定网格中所有格子的数值。可以证明总有解。

第一行包含一个奇数整数 $n$（$3 \le n < 50$），表示网格的边长。

你需要首先读入 $n$。 每次询问关于格子 $(x_1, y_1)$ 和 $(x_2, y_2)$，请在单独一行输出“$?$ $x_1$ $y_1$ $x_2$ $y_2$”。 询问中的数字必须满足 $1 \le x_1 \le x_2 \le n$，$1 \le y_1 \le y_2 \le n$，且 $x_1 + y_1 + 2 \le x_2 + y_2$。不要忘记刷新输出，否则会超时。 对于每次询问，你会收到 $1$，如果存在一条仅向右或向下移动的路径，从 $(x_1, y_1)$ 到 $(x_2, y_2)$，且路径上格子的数字序列构成回文串；否则收到 $0$。 如果你的询问不合法，或者询问次数超过 $n^2$，程序会输出 $-1$ 并终止交互。你会收到 Wrong answer 判定。请立即退出以避免其他判定。 当你确定了所有格子的数值后，输出“!”。 然后输出 $n$ 行，第 $i$ 行为长度为 $n$ 的字符串，表示网格第 $i$ 行的数字。 每次输出询问后不要忘记换行并刷新输出，否则会因输出超时被判为 Idleness limit exceeded。可以使用： - C++：fflush(stdout) 或 cout.flush() - Java：System.out.flush() - Pascal：flush(output) - Python：stdout.flush() - 其它语言请查阅相关文档。 Hack 格式 进行 Hack 时，使用如下格式： 第一行输入一个奇数整数 $n$（网格边长）。 接下来 $n$ 行，每行一个长度为 $n$ 的字符串，表示网格的第 $i$ 行。左上角元素必须为 $1$，右下角元素必须为 $0$。

由 ChatGPT 4.1 翻译