CF1207C Gas Pipeline

你负责沿着一条公路安装燃气管道。为简化问题，我们将公路视为 $OX$ 轴上的一个线段 $[0, n]$。公路上可能有若干个十字路口，但为简化起见，我们将每个十字路口表示为一个区间 $(x, x + 1)$，其中 $x$ 为整数。因此，我们可以用一个长度为 $n$ 的二进制字符串来表示整条公路，其中字符 $0$ 表示当前区间没有十字路口，字符 $1$ 表示该区间有一个十字路口。 通常情况下，我们可以在高度为 $1$ 单位的地方沿公路安装管道，并在每个整数点处设置支柱（也就是说，如果我们负责 $[0, n]$ 的公路，就需要安装 $n + 1$ 根支柱）。但在十字路口处，我们需要将管道抬高到高度 $2$，以免阻碍车辆通行。 我们可以通过插入若干个“之”字形结构来实现抬高。每个“之”字形可以表示为一个区间 $[x, x + 1]$，其中 $x$ 为整数，结构包括三部分：$0.5$ 单位的水平管道 + $1$ 单位的竖直管道 + $0.5$ 单位的水平管道。注意，如果管道当前在高度 $2$，则支撑它的支柱长度也必须为 $2$ 单位。 每单位长度的燃气管道需要 $a$ 布尔币，每单位长度的支柱需要 $b$ 布尔币。因此，将整条管道都架设在高度 $2$ 并不一定最优。请你找出花费最少的管道形状，并计算出该最小花费。 注意，你必须在高度 $1$ 处开始和结束管道，并且保证输入字符串的首尾字符均为 $0$。

第一行包含一个整数 $T$（$1 \le T \le 100$），表示询问的数量。接下来的 $2 \cdot T$ 行，每两行为一个独立的询问。 每个询问的第一行包含三个整数 $n$、$a$、$b$（$2 \le n \le 2 \times 10^5$，$1 \le a \le 10^8$，$1 \le b \le 10^8$），分别表示公路的长度、每单位管道的费用和每单位支柱的费用。 第二行包含一个二进制字符串 $s$（$|s| = n$，$s_i \in \{0, 1\}$，$s_1 = s_n = 0$），表示公路的描述。 保证所有字符串 $s$ 的总长度不超过 $2 \times 10^5$。

输出 $T$ 个整数，每行一个，分别表示每个询问中构建管道的最小可能花费。

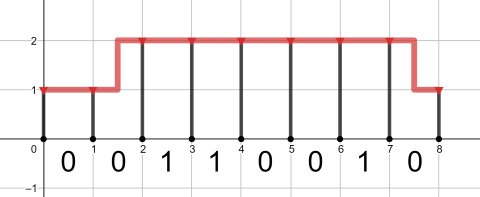
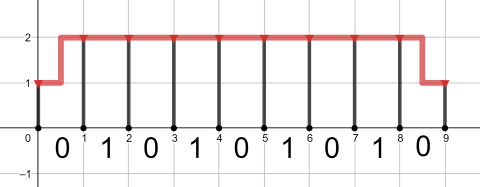
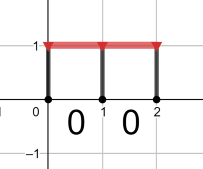
第一个询问的最优管道如上图所示。 第二个询问的最优管道如下图所示：  第三个询问的最优（也是唯一）管道如下图所示：  第四个询问的最优管道如下图所示：  由 ChatGPT 4.1 翻译