CF1207C Gas Pipeline

You are responsible for installing a gas pipeline along a road. Let's consider the road (for simplicity) as a segment $ [0, n] $ on $ OX $ axis. The road can have several crossroads, but for simplicity, we'll denote each crossroad as an interval $ (x, x + 1) $ with integer $ x $ . So we can represent the road as a binary string consisting of $ n $ characters, where character 0 means that current interval doesn't contain a crossroad, and 1 means that there is a crossroad. Usually, we can install the pipeline along the road on height of $ 1 $ unit with supporting pillars in each integer point (so, if we are responsible for $ [0, n] $ road, we must install $ n + 1 $ pillars). But on crossroads we should lift the pipeline up to the height $ 2 $ , so the pipeline won't obstruct the way for cars. We can do so inserting several zig-zag-like lines. Each zig-zag can be represented as a segment $ [x, x + 1] $ with integer $ x $ consisting of three parts: $ 0.5 $ units of horizontal pipe + $ 1 $ unit of vertical pipe + $ 0.5 $ of horizontal. Note that if pipeline is currently on height $ 2 $ , the pillars that support it should also have length equal to $ 2 $ units. Each unit of gas pipeline costs us $ a $ bourles, and each unit of pillar — $ b $ bourles. So, it's not always optimal to make the whole pipeline on the height $ 2 $ . Find the shape of the pipeline with minimum possible cost and calculate that cost. Note that you must start and finish the pipeline on height $ 1 $ and, also, it's guaranteed that the first and last characters of the input string are equal to 0.

The fist line contains one integer $ T $ ( $ 1 \le T \le 100 $ ) — the number of queries. Next $ 2 \cdot T $ lines contain independent queries — one query per two lines. The first line contains three integers $ n $ , $ a $ , $ b $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 1 \le a \le 10^8 $ , $ 1 \le b \le 10^8 $ ) — the length of the road, the cost of one unit of the pipeline and the cost of one unit of the pillar, respectively. The second line contains binary string $ s $ ( $ |s| = n $ , $ s_i \in \{0, 1\} $ , $ s_1 = s_n = 0 $ ) — the description of the road. It's guaranteed that the total length of all strings $ s $ doesn't exceed $ 2 \cdot 10^5 $ .

Print $ T $ integers — one per query. For each query print the minimum possible cost of the constructed pipeline.

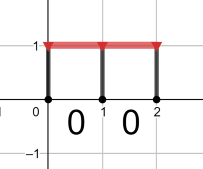
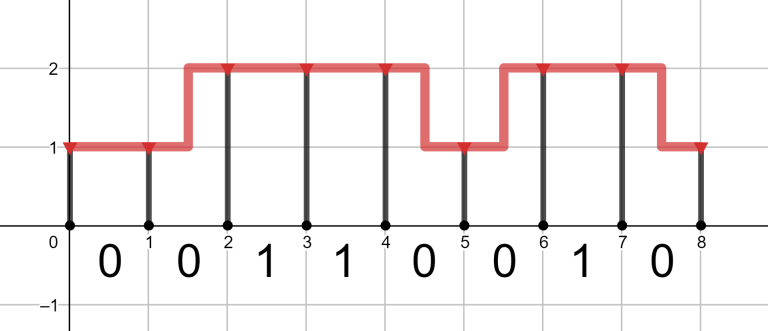
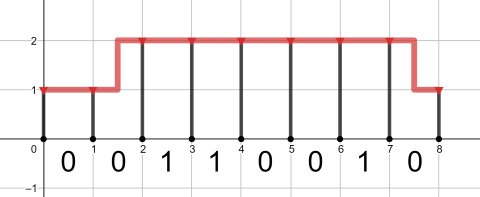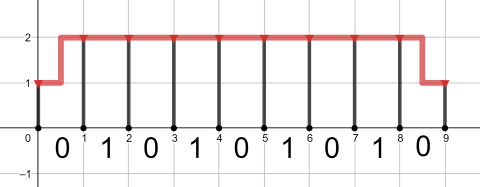The optimal pipeline for the first query is shown at the picture above. The optimal pipeline for the second query is pictured below: The optimal (and the only possible) pipeline for the third query is shown below: The optimal pipeline for the fourth query is shown below: