CF1208E Let Them Slide

给定 $n$ 个长度可以不同的数组。你还有一个有 $w$ 列、$n$ 行的表格。第 $i$ 个数组水平放在第 $i$ 行。你可以在每一行内滑动该数组，只要它占据若干连续的单元格且完全位于表格内即可。 你需要分别独立地求出每一列 $j$（$1 \leq j \leq w$）的最大整数和。 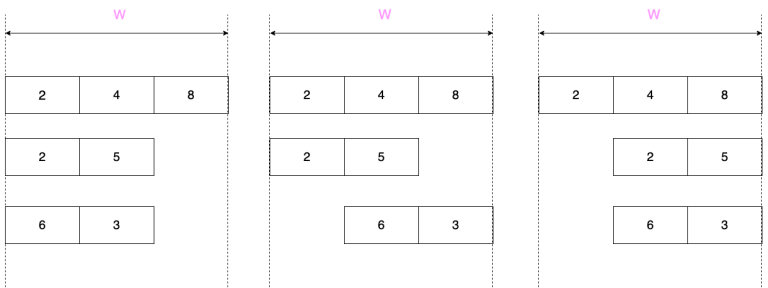 上图从左到右分别展示了第 $1$、$2$、$3$ 列的最优放置方式。注意，只要数组仍在窗口内，你可以让某一列不包含某个数组，此时该数组对该列的贡献视为 $0$。

第一行包含两个整数 $n$（$1 \leq n \leq 10^{6}$）和 $w$（$1 \leq w \leq 10^{6}$），分别表示数组的个数和表格的宽度。 接下来的 $n$ 行，每行包含一个整数 $l_i$（$1 \leq l_i \leq w$），表示第 $i$ 个数组的长度，接着是 $l_i$ 个整数 $a_{i1}, a_{i2}, \ldots, a_{il_i}$（$-10^{9} \leq a_{ij} \leq 10^{9}$），表示数组的元素。 所有数组的总长度不超过 $10^{6}$。

输出 $w$ 个整数，第 $i$ 个表示第 $i$ 列的最大和。

第一个样例的示意图见题面。 由 ChatGPT 4.1 翻译