CF1208G Polygons
题目描述
给定两个整数 $n$ 和 $k$。
你需要构造 $k$ 个正多边形,这些多边形拥有相同的外接圆,且每个多边形的边数 $l$ 互不相同,满足 $3 \leq l \leq n$。
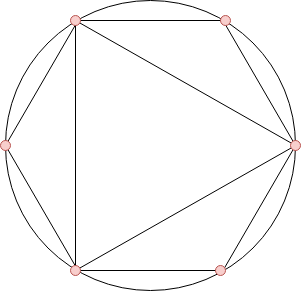
上图为第一个样例的示意图。你可以通过旋转多边形来最小化圆上不同点的总数。请你求出所需的最小点数。
输入格式
输入仅一行,包含两个整数 $n$ 和 $k$($3 \leq n \leq 10^{6}$,$1 \leq k \leq n-2$),分别表示多边形的最大边数和需要构造的多边形数量。
输出格式
输出一个整数,表示构造 $k$ 个多边形所需的最小点数。
说明/提示
在第一个样例中,$n = 6$,$k = 2$。因此,我们可以从边数为 $3$、$4$、$5$、$6$ 的多边形中任选两个。如果选择三角形和六边形,则可以如题目图片所示进行排列。
因此,所需的最小点数为 $6$,这也是所有可能集合中的最小值。
由 ChatGPT 4.1 翻译