CF1208G Polygons

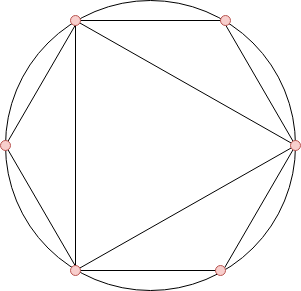
给定两个整数 $n$ 和 $k$。 你需要构造 $k$ 个正多边形，这些多边形拥有相同的外接圆，且每个多边形的边数 $l$ 互不相同，满足 $3 \leq l \leq n$。  上图为第一个样例的示意图。你可以通过旋转多边形来最小化圆上不同点的总数。请你求出所需的最小点数。

输入仅一行，包含两个整数 $n$ 和 $k$（$3 \leq n \leq 10^{6}$，$1 \leq k \leq n-2$），分别表示多边形的最大边数和需要构造的多边形数量。

输出一个整数，表示构造 $k$ 个多边形所需的最小点数。

在第一个样例中，$n = 6$，$k = 2$。因此，我们可以从边数为 $3$、$4$、$5$、$6$ 的多边形中任选两个。如果选择三角形和六边形，则可以如题目图片所示进行排列。 因此，所需的最小点数为 $6$，这也是所有可能集合中的最小值。 由 ChatGPT 4.1 翻译