CF1208H Red Blue Tree

You are given a tree of $ n $ nodes. The tree is rooted at node $ 1 $ , which is not considered as a leaf regardless of its degree. Each leaf of the tree has one of the two colors: red or blue. Leaf node $ v $ initially has color $ s_{v} $ . The color of each of the internal nodes (including the root) is determined as follows. - Let $ b $ be the number of blue immediate children, and $ r $ be the number of red immediate children of a given vertex. - Then the color of this vertex is blue if and only if $ b - r \ge k $ , otherwise red. Integer $ k $ is a parameter that is same for all the nodes. You need to handle the following types of queries: - 1 v: print the color of node $ v $ ; - 2 v c: change the color of leaf $ v $ to $ c $ ( $ c = 0 $ means red, $ c = 1 $ means blue); - 3 h: update the current value of $ k $ to $ h $ .

The first line of the input consists of two integers $ n $ and $ k $ ( $ 2 \le n \le 10^{5} $ , $ -n \le k \le n $ ) — the number of nodes and the initial parameter $ k $ . Each of the next $ n - 1 $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ ), denoting that there is an edge between vertices $ u $ and $ v $ . The next line consists of $ n $ space separated integers — the initial array $ s $ ( $ -1 \le s_i \le 1 $ ). $ s_{i} = 0 $ means that the color of node $ i $ is red. $ s_{i} = 1 $ means that the color of node $ i $ is blue. $ s_{i} = -1 $ means that the node $ i $ is not a leaf. The next line contains an integer $ q $ ( $ 1 \le q \le 10^5 $ ), the number of queries. $ q $ lines follow, each containing a query in one of the following queries: - 1 v ( $ 1 \le v \le n $ ): print the color of node $ v $ ; - 2 v c ( $ 1 \le v \le n $ , $ c = 0 $ or $ c = 1 $ ): change the color of leaf $ v $ to $ c $ ( $ c = 0 $ means red, $ c = 1 $ means blue). It is guaranteed that $ v $ is a leaf; - 3 h ( $ -n \le h \le n $ ): update the current value of $ k $ to $ h $ .

For each query of the first type, print $ 0 $ if the color of vertex $ v $ is red, and $ 1 $ otherwise.

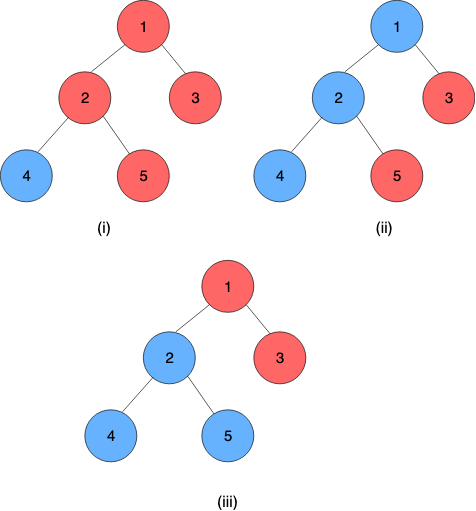
Figures:(i) The initial tree (ii) The tree after the 3rd query (iii) The tree after the 7th query