CF1208H Red Blue Tree

给定一棵包含 $n$ 个节点的树。树以节点 $1$ 为根，无论其度数如何，节点 $1$ 都不被视为叶子节点。 树的每个叶子节点有两种颜色之一：红色或蓝色。叶子节点 $v$ 的初始颜色为 $s_{v}$。 每个内部节点（包括根节点）的颜色由以下规则确定： - 设 $b$ 为某顶点的蓝色直接子节点数量，$r$ 为红色直接子节点数量。 - 当且仅当 $b - r \ge k$ 时，该顶点为蓝色，否则为红色。 整数 $k$ 是全局参数，对所有节点相同。 需要处理以下类型的查询： 1. `1 v`：输出节点 $v$ 的颜色； 2. `2 v c`：将叶子节点 $v$ 的颜色改为 $c$（$c = 0$ 表示红色，$c = 1$ 表示蓝色）； 3. `3 h`：将当前参数 $k$ 更新为 $h$。

输入的第一行包含两个整数 $n$ 和 $k$（$2 \le n \le 10^{5}$，$-n \le k \le n$）——节点数量和初始参数 $k$。 接下来的 $n - 1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$），表示节点 $u$ 和 $v$ 之间有一条边。 接下来一行包含 $n$ 个用空格分隔的整数——初始数组 $s$（$-1 \le s_i \le 1$）。$s_{i} = 0$ 表示节点 $i$ 为红色，$s_{i} = 1$ 表示蓝色，$s_{i} = -1$ 表示节点 $i$ 不是叶子。 下一行包含一个整数 $q$（$1 \le q \le 10^5$），表示查询数量。 随后 $q$ 行，每行为以下查询之一： - `1 v`（$1 \le v \le n$）：输出节点 $v$ 的颜色； - `2 v c`（$1 \le v \le n$，$c = 0$ 或 $c = 1$）：将叶子节点 $v$ 的颜色改为 $c$（保证 $v$ 是叶子节点）； - `3 h`（$-n \le h \le n$）：将当前参数 $k$ 更新为 $h$。

对于每个类型 `1` 的查询，若节点 $v$ 为红色则输出 $0$，否则输出 $1$。

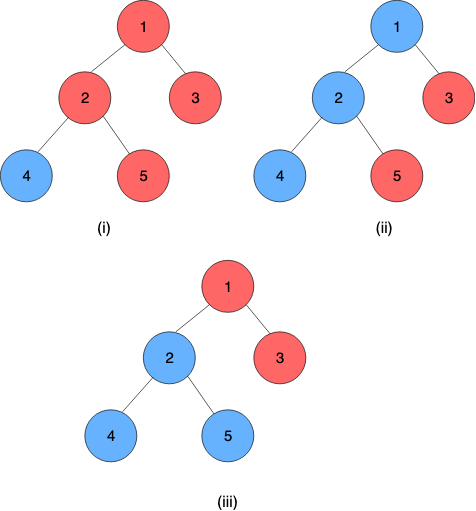
图示： (i) 初始树 (ii) 第 3 次查询后的树 (iii) 第 7 次查询后的树  翻译由 DeepSeek V3 完成