CF1209B Koala and Lights

It is a holiday season, and Koala is decorating his house with cool lights! He owns $ n $ lights, all of which flash periodically. After taking a quick glance at them, Koala realizes that each of his lights can be described with two parameters $ a_i $ and $ b_i $ . Light with parameters $ a_i $ and $ b_i $ will toggle (on to off, or off to on) every $ a_i $ seconds starting from the $ b_i $ -th second. In other words, it will toggle at the moments $ b_i $ , $ b_i + a_i $ , $ b_i + 2 \cdot a_i $ and so on. You know for each light whether it's initially on or off and its corresponding parameters $ a_i $ and $ b_i $ . Koala is wondering what is the maximum number of lights that will ever be on at the same time. So you need to find that out. 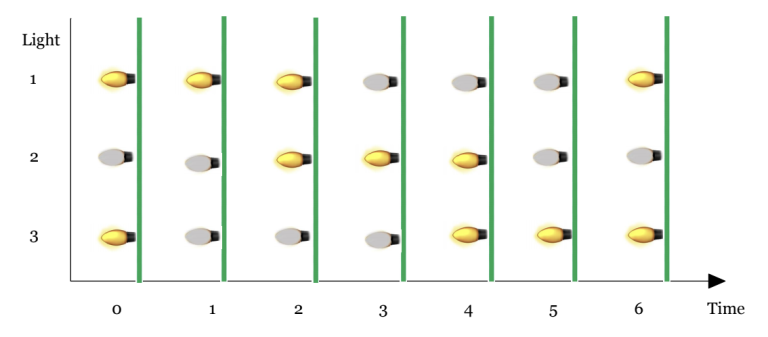Here is a graphic for the first example.

The first line contains a single integer $ n $ ( $ 1 \le n \le 100 $ ), the number of lights. The next line contains a string $ s $ of $ n $ characters. The $ i $ -th character is "1", if the $ i $ -th lamp is initially on. Otherwise, $ i $ -th character is "0". The $ i $ -th of the following $ n $ lines contains two integers $ a_i $ and $ b_i $ ( $ 1 \le a_i, b_i \le 5 $ ) — the parameters of the $ i $ -th light.

Print a single integer — the maximum number of lights that will ever be on at the same time.

For first example, the lamps' states are shown in the picture above. The largest number of simultaneously on lamps is $ 2 $ (e.g. at the moment $ 2 $ ). In the second example, all lights are initially on. So the answer is $ 4 $ .