CF1209H Moving Walkways

机场常常使用自动步道帮助你更快地走完较长的距离。每条自动步道都有一定的速度，可以有效提升你的移动速度。你可以站在步道上让它带着你移动，也可以在步道上行走，此时你的实际速度等于你的行走速度加上步道的速度。 Limak 想要从 $0$ 点走到 $L$ 点，这是一条直线。在这之间有 $n$ 条互不重叠的自动步道。第 $i$ 条步道由两个整数 $x_i$ 和 $y_i$ 以及一个实数 $s_i$ 描述。第 $i$ 条步道从 $x_i$ 开始，到 $y_i$ 结束，速度为 $s_i$。 每条步道都位于区间 $[0, L]$ 内，且任意两条步道没有正交集，但它们的端点可以相接。 Limak 需要合理分配自己的体力。例如，有时站着不动（或者慢慢走）可以让他积攒更多体力，以便之后能更快地行走。 Limak 的初始体力为 $0$，且体力值不能降到 $0$ 以下。任意时刻，他都可以以任意速度 $v$（$0 \le v \le 2$）行走，每秒消耗 $v$ 点体力，但他会以每秒 $1$ 点的速度持续恢复体力。因此，当他以速度 $v$ 行走时，每秒体力变化为 $1-v$。注意，负值表示体力在减少。 特别地，他可以以速度 $1$ 行走，这样体力不会变化；以速度 $0.77$ 行走，每秒还能恢复 $0.23$ 点体力。 Limak 可以在任意时刻自由选择速度（$[0, 2]$ 区间内的任意实数），包括在非整数位置时。所有过程都是连续的。 Limak 最快能用多长时间从 $0$ 走到 $L$？

第一行包含两个整数 $n$ 和 $L$（$1 \le n \le 200\,000$，$1 \le L \le 10^9$），分别表示自动步道的数量和总距离。 接下来的 $n$ 行，每行包含两个整数 $x_i$、$y_i$ 和一个实数 $s_i$（$0 \le x_i < y_i \le L$，$0.1 \le s_i \le 10.0$）。$s_i$ 最多保留 $9$ 位小数。 保证任意两条步道没有正交集，且步道按从左到右顺序给出，即 $y_i \le x_{i+1}$ 对于 $1 \le i \le n-1$ 成立。

输出一个实数，表示到达 $L$ 的最短时间。若你的答案的绝对误差或相对误差不超过 $10^{-9}$，则视为正确。

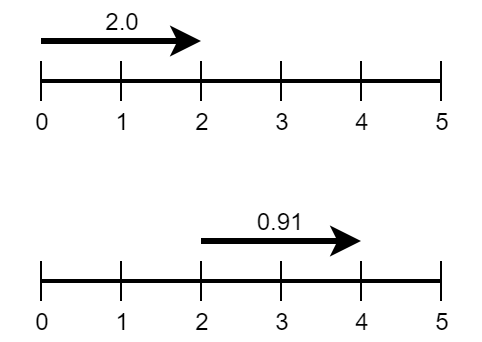
下图展示了前两个样例。在第一个样例中，有一条从 $0$ 到 $2$ 的步道，速度为 $2.0$，Limak 需要到达 $5$ 点。第二个样例有一条从 $2$ 到 $4$ 的步道，速度为 $0.91$。  在第一个样例中，一种最优策略如下： - 从 $0$ 到 $2$，站在步道上不动。步道以 $2$ 的速度带着你前进，需要 $1$ 秒，同时你积攒了 $1$ 点体力。 - 从 $2$ 到 $4$，以最大速度 $2$ 行走，用时 $1$ 秒，体力降为 $0$。 - 从 $4$ 到 $5$，以速度 $1$ 行走，用时 $1$ 秒，体力保持为 $0$。 总时间为 $1+1+1=3$。 由 ChatGPT 4.1 翻译