CF120J Minimum Sum

You are given a set of $ n $ vectors on a plane. For each vector you are allowed to multiply any of its coordinates by -1. Thus, each vector $ v_{i}=(x_{i},y_{i}) $ can be transformed into one of the following four vectors: - $ v_{i}^{1}=(x_{i},y_{i}) $ , - $ v_{i}^{2}=(-x_{i},y_{i}) $ , - $ v_{i}^{3}=(x_{i},-y_{i}) $ , - $ v_{i}^{4}=(-x_{i},-y_{i}) $ . You should find two vectors from the set and determine which of their coordinates should be multiplied by -1 so that the absolute value of the sum of the resulting vectors was minimally possible. More formally, you should choose two vectors $ v_{i} $ , $ v_{j} $ ( $ 1

The first line contains a single integer $ n $ ( $ 2

Print on the first line four space-separated numbers " $ i $ $ k_{1} $ $ j $ $ k_{2} $ " — the answer to the problem. If there are several variants the absolute value of whose sums is minimum, you can print any of them.

A sum of two vectors $ v=(x_{v},y_{v}) $ and $ u=(x_{u},y_{u}) $ is vector $ s=v+u=(x_{v}+x_{u},y_{v}+y_{u}) $ . An absolute value of vector $ v=(x,y) $ is number 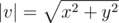. In the second sample there are several valid answers, such as: (3 1 4 2), (3 1 4 4), (3 4 4 1), (3 4 4 3), (4 1 3 2), (4 1 3 4), (4 2 3 1).