CF1210C Kamil and Making a Stream

Kamil 喜欢观看竞技编程的视频。他的 MeTube 频道最近达到了 $100$ 万订阅者。为了庆祝这一时刻，他发布了一个有趣但自己还未能解决的问题。你能帮助他吗？ 给定一棵树——一个包含 $n$ 个顶点、由 $n-1$ 条边连接而成的连通无向图。树的根为顶点 $1$。如果顶点 $u$ 位于从根到顶点 $v$ 的最短路径上，则称 $u$ 是 $v$ 的祖先。特别地，一个顶点也是它自身的祖先。 每个顶点 $v$ 被赋予一个美丽值 $x_v$，它是一个不超过 $10^{12}$ 的非负整数。基于此，我们可以定义一条路径的美丽值。设 $u$ 是 $v$ 的祖先，则路径的美丽值 $f(u, v)$ 定义为从 $u$ 到 $v$ 的最短路径上所有顶点美丽值的最大公约数。形式化地，若 $u = t_1, t_2, t_3, \dots, t_k = v$ 是从 $u$ 到 $v$ 的最短路径上的顶点，则 $f(u, v) = \gcd(x_{t_1}, x_{t_2}, \dots, x_{t_k})$。这里 $\gcd$ 表示一组数的最大公约数。特别地，$f(u, u) = \gcd(x_u) = x_u$。 你的任务是计算如下和： $$ \sum_{u\text{ 是 }v\text{ 的祖先}} f(u, v) $$ 由于结果可能过大，请输出对 $10^9 + 7$ 取模后的答案。 注意，对于任意 $y$，有 $\gcd(0, y) = \gcd(y, 0) = y$。特别地，$\gcd(0, 0) = 0$。

第一行包含一个整数 $n$（$2 \le n \le 100\,000$），表示树的顶点数。 第二行包含 $n$ 个整数 $x_1, x_2, \dots, x_n$（$0 \le x_i \le 10^{12}$），其中 $x_v$ 表示顶点 $v$ 的美丽值。 接下来的 $n-1$ 行描述树的边。每行包含两个整数 $a, b$（$1 \le a, b \le n$，$a \neq b$），表示顶点 $a$ 和顶点 $b$ 之间有一条边。

输出所有满足 $u$ 是 $v$ 的祖先的路径 $(u, v)$ 的美丽值之和。答案对 $10^9 + 7$ 取模。

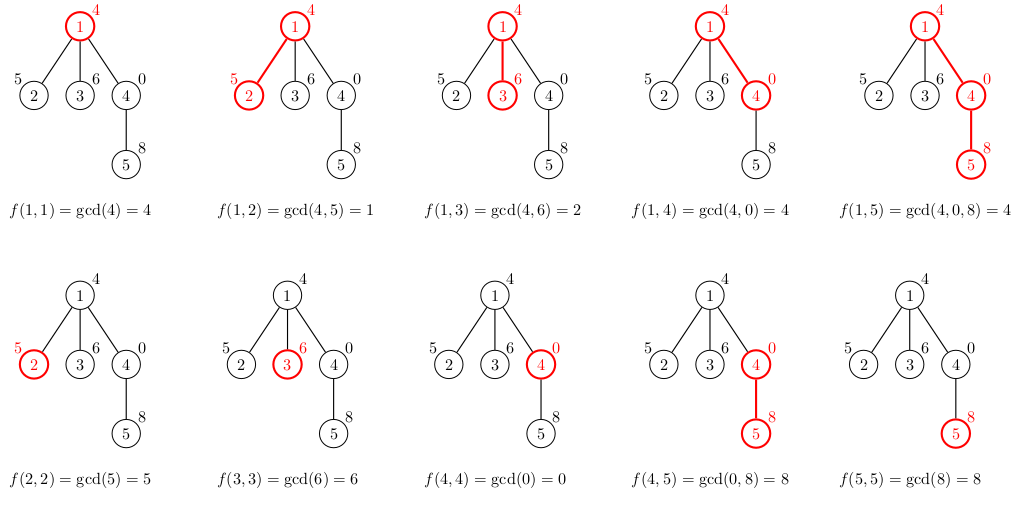
下图展示了所有 $10$ 条以一个端点为另一个端点祖先的路径。所有这些路径的美丽值之和为 $42$：  由 ChatGPT 4.1 翻译