CF1210C Kamil and Making a Stream

Kamil likes streaming the competitive programming videos. His MeTube channel has recently reached $ 100 $ million subscribers. In order to celebrate this, he posted a video with an interesting problem he couldn't solve yet. Can you help him? You're given a tree — a connected undirected graph consisting of $ n $ vertices connected by $ n - 1 $ edges. The tree is rooted at vertex $ 1 $ . A vertex $ u $ is called an ancestor of $ v $ if it lies on the shortest path between the root and $ v $ . In particular, a vertex is an ancestor of itself. Each vertex $ v $ is assigned its beauty $ x_v $ — a non-negative integer not larger than $ 10^{12} $ . This allows us to define the beauty of a path. Let $ u $ be an ancestor of $ v $ . Then we define the beauty $ f(u, v) $ as the greatest common divisor of the beauties of all vertices on the shortest path between $ u $ and $ v $ . Formally, if $ u=t_1, t_2, t_3, \dots, t_k=v $ are the vertices on the shortest path between $ u $ and $ v $ , then $ f(u, v) = \gcd(x_{t_1}, x_{t_2}, \dots, x_{t_k}) $ . Here, $ \gcd $ denotes the greatest common divisor of a set of numbers. In particular, $ f(u, u) = \gcd(x_u) = x_u $ . Your task is to find the sum $ $$$ \sum_{u\text{ is an ancestor of }v} f(u, v). $ $

As the result might be too large, please output it modulo $ 10^9 + 7 $ .

Note that for each $ y $ , $ \\gcd(0, y) = \\gcd(y, 0) = y $ . In particular, $ \\gcd(0, 0) = 0$$$.

The first line contains a single integer $ n $ ( $ 2 \le n \le 100\,000 $ ) — the number of vertices in the tree. The following line contains $ n $ integers $ x_1, x_2, \dots, x_n $ ( $ 0 \le x_i \le 10^{12} $ ). The value $ x_v $ denotes the beauty of vertex $ v $ . The following $ n - 1 $ lines describe the edges of the tree. Each of them contains two integers $ a, b $ ( $ 1 \le a, b \le n $ , $ a \neq b $ ) — the vertices connected by a single edge.

Output the sum of the beauties on all paths $ (u, v) $ such that $ u $ is ancestor of $ v $ . This sum should be printed modulo $ 10^9 + 7 $ .

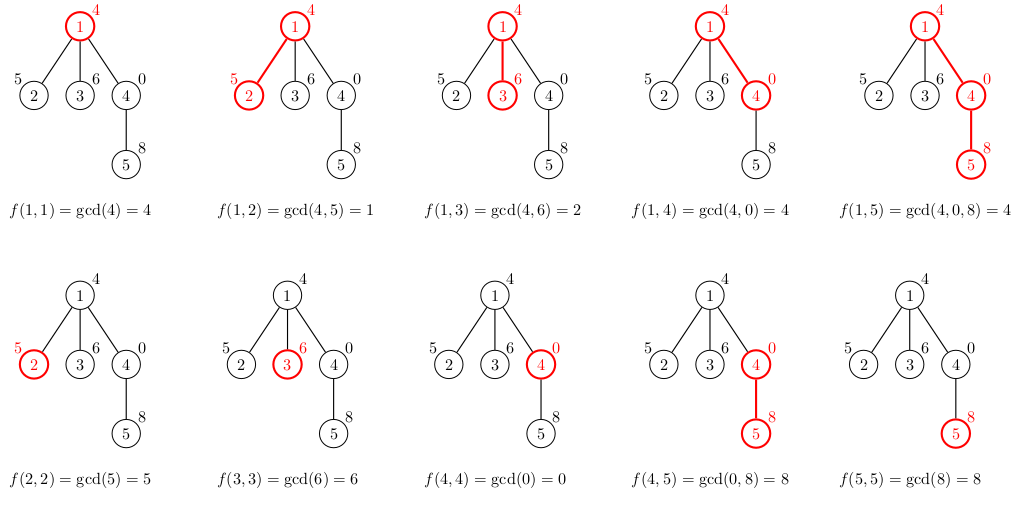
The following figure shows all $ 10 $ possible paths for which one endpoint is an ancestor of another endpoint. The sum of beauties of all these paths is equal to $ 42 $ :