CF1211G King's Path

树之国有n个城市和n-1条双向道路。每条路连接着两个不同的城市。你可以从任何一个城市开车到另一个城市，只需要沿着道路行驶。城市的编号从1到n。当然，你在这个描述中认出了一棵无向树。 每个城市都有一面国旗，在第 i 个城市，国旗的颜色是$c_i$。不同城市的国旗颜色可能是一样的。 如果国王旅行沿途 [$u_1$,$u_2$,$u_3$,...,$u_k$] 那么这就意味着,他开始在城市 $u_1$ ,然后移动到城市$u_2$ ($u_2$与$u_1$之间有公路连接) ,然后从$u_2$到$u_3$ ($u_3$与$u_2$之间有公路连接),直到他到达城市$u_k$。在这条路线上，国王可能会多次访问同一个城市。换句话说，路线[$u_1$,$u_2$,$u_3$,...,$u_k$]不一定由不同的城市组成。在图论方面，国王沿着一些路径 [$u_1$,$u_2$,$u_3$,...,$u_k$] 从$u_1$移动到$u_k$，这并不一定简单(对于城市 $u_j$ 和$u_{j+1}$(所有 j 取于1到k-1)都是通过道路连接的)。 当国王从一个城市到另一个城市时，城市领导人交换旗帜作为他们友谊的标志。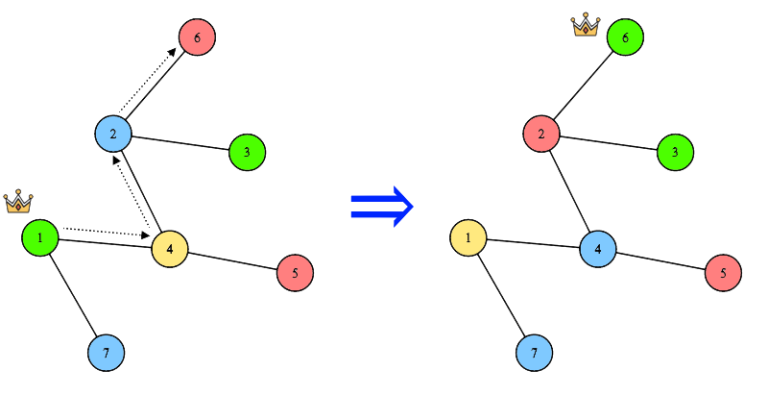  例： 移动国王沿路线[1,4,2,6]。顶点的颜色与该顶点的标志颜色相匹配。出于美观的原因，国王希望城市$d_i$(1$\le$i$\le$n)的旗帜颜色都是相同的。确定国王是否可以选择一些路线并沿着它行驶，以便每个城市的旗帜颜色都与期望的颜色相同。**注意，国王可以选择(并驾驶)一条路线。如果是，为国王找一条最短的路线。** 如果旗子的初始颜色已经符合国王的要求(即对于所有i,$c_i$=$d_i$)，则认为国王的路线长度为k=0。

第一行包含一个整数 t (1$\le$t$\le$$10^5$)——要解决的测试用例的数量。 每一种情况先输入一个整数n (2$\le$n$\le$$2⋅10^5$)即树之国的城市数量。 下面输入n个整数，$c_1$,$c_2$,...,$c_n$(1$\le$$c_i$$\le$$10^6$)，其中$c_i$表示国王旅行前第i个顶点的旗帜颜色。 下面是一行n个整数,$d_1$,$d_2$,...,$d_n$(1$\le$$d_i$$\le$$10^6$)，其中$d_i$表示国王旅程完成后第i个顶点所需的旗帜颜色。 此外，在n−1行，列出树地的道路。每条道路连接两个整数点$x_j$,$y_j$(1$\le$$x_j$,$y_j$$\le$n) ——由第j条道路连接的城市数量。 它保证从每个城市你都可以通过道路到达任何其他城市(换句话说，城市和道路系统形成了一个无向树)。 在一次测试中，所有情况下所有n值的总和不超过$2⋅10 ^5$。

按输入数据中出现的顺序输出所有案例的答案。 每个答案必须以包含“Yes”(在肯定答案的情况下)或“No”(在所要求的路线不存在的情况下)。如果答案是肯定的，下面一行必须包含一个整数k——国王最短可能路线上的城市数量。下一行应该包含所需的路线$u_1$,$u_2$,...,$u_k$(1$\le$$u_i$$\le$n)。如果k=0，可以跳过这行。