CF1214H Tiles Placement

莫斯科市中心的新步行区由 $n$ 个广场组成，这些广场通过 $n-1$ 条人行道相连。我们定义一条简单路径为一系列广场的序列，序列中没有任何广场重复出现，并且序列中任意相邻的两个广场都通过一条人行道直接相连。简单路径的大小为其中包含的广场数。人行道的设计保证了任意两个不同的广场之间恰好有一条简单路径。 在为莫斯科城市日做准备时，市议会决定为所有 $n$ 个广场更换地砖。共有 $k$ 种不同颜色的地砖，编号为 $1$ 到 $k$。每个广场必须选择且仅选择一种地砖类型来铺设。为了让市中心的步行体验更加有趣，要求为每个广场选择地砖类型，使得任意一条大小恰好为 $k$ 的简单路径都包含所有 $k$ 种不同颜色的地砖。 你需要判断是否存在一种地砖铺设方案满足上述要求。

第一行包含两个整数 $n$ 和 $k$（$2 \le k \le n \le 200\,000$），分别表示新步行区的广场数和不同地砖颜色的数量。 接下来的 $n-1$ 行，每行包含两个整数 $v_i$ 和 $u_i$（$1 \le v_i, u_i \le n$），表示第 $i$ 条人行道连接的两个广场编号。 保证任意两个广场之间都可以互相到达，并且恰好有一条简单路径。

如果存在满足条件的地砖铺设方案，输出 "Yes"；否则输出 "No"。 如果你的答案是 "Yes"，请在下一行输出 $n$ 个整数，每个整数在 $1$ 到 $k$ 之间，依次表示每个广场的地砖颜色。

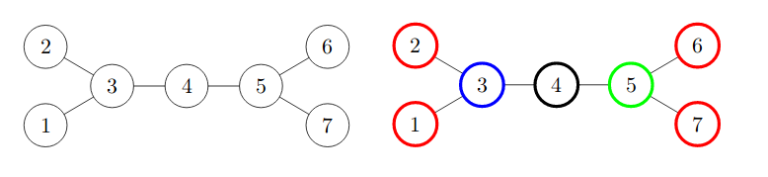
下图展示了第一个和第二个样例中步行区的结构。第二张图还展示了 $k=4$ 时的一种可能的颜色分配方案。  由 ChatGPT 4.1 翻译