CF1218B Guarding warehouses

Bob Bubblestrong 刚刚获得了一份新的工作，成为了一名保安。现在，Bob 负责一批仓库的安全，每个仓库都存放着最珍贵的 Bubble Cup 资产——高品质的泡泡。他的任务是发现仓库内的窃贼并报警。 从空中俯视，每个仓库的形状都是一个凸多边形。任意两个仓库的墙壁不会相交，当然，也没有任何一个仓库建在另一个仓库内部。 Bubble Cup 的老板们并不知道 Bob 有多懒，他喜欢在办公室的舒适环境中看肥皂剧（他听说里面充满了泡泡）。Bob 的计划是，利用特殊的 X 射线眼镜，在办公室里监控所有仓库，而不是亲自去每个仓库巡查。眼镜的射程无限，因此可以轻松发现任何仓库里的小偷。 然而，眼镜很快就坏了，现在 X 射线只能穿透一堵墙。现在，Bob 非常希望你能帮他计算一下，通过坏掉的眼镜，他能监控到的所有仓库内部的总面积，这样他就能知道还需要亲自巡查多少仓库面积了。

第一行包含一个整数 $N$（$1 \leq N \leq 10^4$），表示仓库的数量。 接下来的 $N$ 行描述每个仓库。 每行的第一个数字是整数 $c_i$（$3 \leq c_i \leq 10^4$），表示第 $i$ 个仓库的顶点数，接下来是 $c_i$ 对整数。第 $j$ 对为 $(x_j, y_j)$，表示第 $j$ 个顶点的坐标（$|x_j|, |y_j| \leq 3 \times 10^4$）。顶点按顺时针顺序给出。所有仓库的顶点总数不超过 $5 \times 10^4$。 Bob 的办公室位于坐标 $(0, 0)$。办公室不在任何一个仓库内部。

输出一行，包含一个至少保留四位小数的实数，表示 Bob 通过坏掉的 X 射线眼镜能监控到的所有仓库内部的总面积。

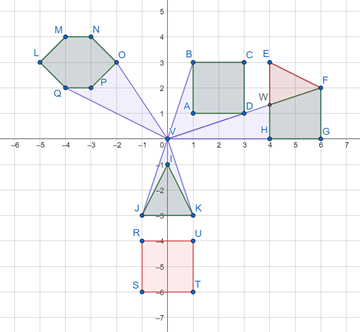
 被 X 射线眼镜监控到的区域用绿色表示，未被监控到的区域用红色表示。 仓库 $ABCD$、$IJK$ 和 $LMNOPQ$ 能被眼镜完全监控。 仓库 $EFGH$ 能被部分监控：区域 $EFW$ 未被监控，因为要监控该区域内的每一点，X 射线都必须穿过仓库 $ABCD$ 的两堵墙。 仓库 $RUTS$ 完全无法从 Bob 的办公室监控，因为在办公室与该仓库内任意一点之间，都有仓库 $IJK$ 的两堵墙。 被眼镜监控到的总面积 $P = P_{ABCD} + P_{FGHW} + P_{IJK} + P_{LMNOPQ} = 4 + 3.333333333333 + 2 + 4 = 13.333333333333$。 由 ChatGPT 4.1 翻译