CF1228B Filling the Grid

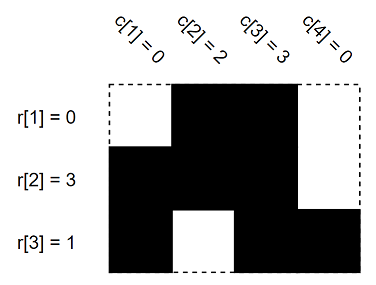
假设有一个 $h \times w$ 的网格，每个格子可以是空的或填满的。我们做如下定义： - $r_{i}$ 表示第 $i$ 行（$1 \le i \le h$）从左侧开始连续填满的格子的数量。特别地，如果第 $i$ 行最左侧的格子是空的，则 $r_i=0$。 - $c_{j}$ 表示第 $j$ 列（$1 \le j \le w$）从上端开始连续填满的格子的数量。特别地，如果第 $j$ 列最上面的格子是空的，则 $c_j=0$。 换句话说，第 $i$ 行恰好以 $r_i$ 个连续填满的格子开始。类似地，第 $j$ 列恰好以 $c_j$ 个连续填满的格子开始。  上图是某个 $3 \times 4$ 网格的 $r$ 和 $c$ 值。黑色格子表示填满，白色格子表示空。 现在给定 $r$ 和 $c$ 的值。初始时所有格子都是空的。请你计算有多少种填充格子的方案可以满足 $r$ 和 $c$ 的要求。由于答案可能非常大，请输出答案对 $1000000007\,(10^{9} + 7)$ 取模后的结果。 换句话说，输出答案除以 $1000000007\,(10^{9} + 7)$ 的余数。

第一行包含两个整数 $h$ 和 $w$（$1 \le h, w \le 10^{3}$），表示网格的高度和宽度。 第二行包含 $h$ 个整数 $r_{1}, r_{2}, \ldots, r_{h}$（$0 \le r_{i} \le w$），表示每一行的 $r$ 值。 第三行包含 $w$ 个整数 $c_{1}, c_{2}, \ldots, c_{w}$（$0 \le c_{j} \le h$），表示每一列的 $c$ 值。

输出满足条件的方案数，对 $1000000007\,(10^{9} + 7)$ 取模后的结果。

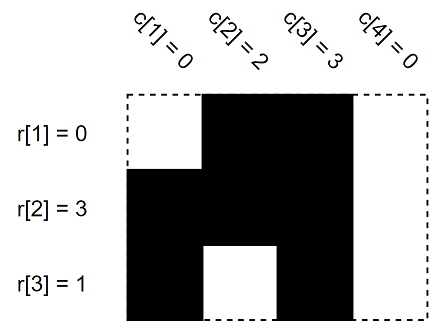
在第一个样例中，下面是另一种可能的填充方式。  在第二个样例中，不存在任何一种填充方式可以同时满足给定的 $r$ 和 $c$ 值。 在第三个样例中，记得输出答案对 $(10^9 + 7)$ 取模后的结果。 由 ChatGPT 4.1 翻译