CF1228D Complete Tripartite

You have a simple undirected graph consisting of $ n $ vertices and $ m $ edges. The graph doesn't contain self-loops, there is at most one edge between a pair of vertices. The given graph can be disconnected. Let's make a definition. Let $ v_1 $ and $ v_2 $ be two some nonempty subsets of vertices that do not intersect. Let $ f(v_{1}, v_{2}) $ be true if and only if all the conditions are satisfied: 1. There are no edges with both endpoints in vertex set $ v_1 $ . 2. There are no edges with both endpoints in vertex set $ v_2 $ . 3. For every two vertices $ x $ and $ y $ such that $ x $ is in $ v_1 $ and $ y $ is in $ v_2 $ , there is an edge between $ x $ and $ y $ . Create three vertex sets ( $ v_{1} $ , $ v_{2} $ , $ v_{3} $ ) which satisfy the conditions below; 1. All vertex sets should not be empty. 2. Each vertex should be assigned to only one vertex set. 3. $ f(v_{1}, v_{2}) $ , $ f(v_{2}, v_{3}) $ , $ f(v_{3}, v_{1}) $ are all true. Is it possible to create such three vertex sets? If it's possible, print matching vertex set for each vertex.

The first line contains two integers $ n $ and $ m $ ( $ 3 \le n \le 10^{5} $ , $ 0 \le m \le \text{min}(3 \cdot 10^{5}, \frac{n(n-1)}{2}) $ ) — the number of vertices and edges in the graph. The $ i $ -th of the next $ m $ lines contains two integers $ a_{i} $ and $ b_{i} $ ( $ 1 \le a_{i} \lt b_{i} \le n $ ) — it means there is an edge between $ a_{i} $ and $ b_{i} $ . The graph doesn't contain self-loops, there is at most one edge between a pair of vertices. The given graph can be disconnected.

If the answer exists, print $ n $ integers. $ i $ -th integer means the vertex set number (from $ 1 $ to $ 3 $ ) of $ i $ -th vertex. Otherwise, print $ -1 $ . If there are multiple answers, print any.

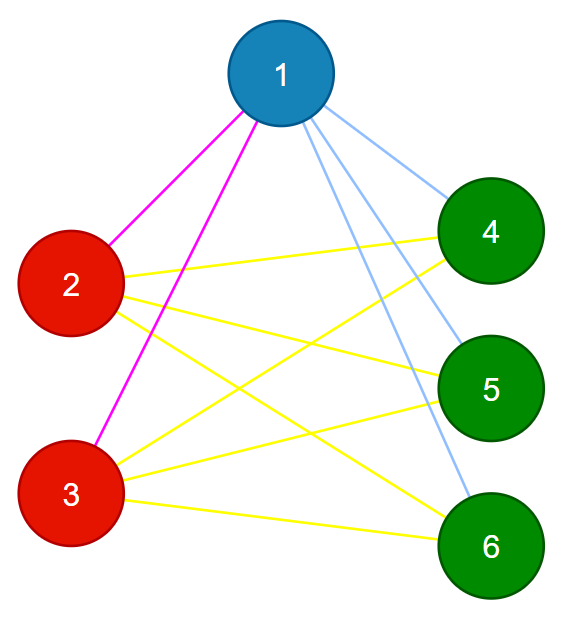In the first example, if $ v_{1} = \{ 1 \} $ , $ v_{2} = \{ 2, 3 \} $ , and $ v_{3} = \{ 4, 5, 6 \} $ then vertex sets will satisfy all conditions. But you can assign vertices to vertex sets in a different way; Other answers like "2 3 3 1 1 1" will be accepted as well. In the second example, it's impossible to make such vertex sets.