CF1228E Another Filling the Grid
题目描述
给定一个 $n \times n$ 的正方形网格和一个整数 $k$。请在每个格子中填入一个整数,要求满足以下条件:
- 网格中所有数字都在 $1$ 到 $k$ 之间(包含 $1$ 和 $k$)。
- 第 $i$ 行的最小值为 $1$($1 \le i \le n$)。
- 第 $j$ 列的最小值为 $1$($1 \le j \le n$)。
请计算有多少种填数方案。由于答案可能非常大,请输出答案对 $10^9+7$ 取模后的结果。
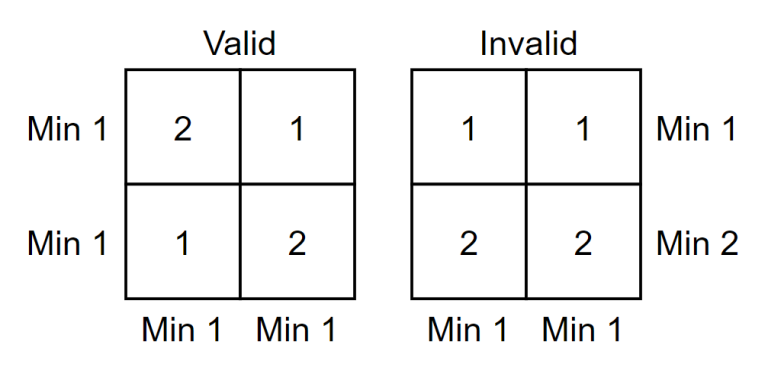 上图为 $n=k=2$ 时,合法和不合法的网格示例。
输入格式
一行输入两个整数 $n$ 和 $k$,满足 $1 \le n \le 250$,$1 \le k \le 10^9$。
输出格式
输出一个整数,表示方案数对 $10^9+7$ 取模后的结果。
说明/提示
在第一个样例中,共有 $7$ 种合法方案。
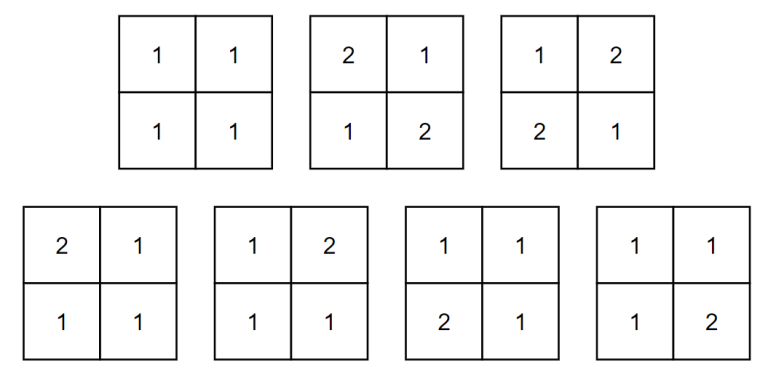 在第二个样例中,请确保输出的答案对 $10^9+7$ 取模。
由 ChatGPT 4.1 翻译