CF1228F One Node is Gone

You have an integer $ n $ . Let's define following tree generation as McDic's generation: 1. Make a complete and full binary tree of $ 2^{n} - 1 $ vertices. Complete and full binary tree means a tree that exactly one vertex is a root, all leaves have the same depth (distance from the root), and all non-leaf nodes have exactly two child nodes. 2. Select a non-root vertex $ v $ from that binary tree. 3. Remove $ v $ from tree and make new edges between $ v $ 's parent and $ v $ 's direct children. If $ v $ has no children, then no new edges will be made. You have a tree. Determine if this tree can be made by McDic's generation. If yes, then find the parent vertex of removed vertex in tree.

The first line contains integer $ n $ ( $ 2 \le n \le 17 $ ). The $ i $ -th of the next $ 2^{n} - 3 $ lines contains two integers $ a_{i} $ and $ b_{i} $ ( $ 1 \le a_{i} \lt b_{i} \le 2^{n} - 2 $ ) — meaning there is an edge between $ a_{i} $ and $ b_{i} $ . It is guaranteed that the given edges form a tree.

Print two lines. In the first line, print a single integer — the number of answers. If given tree cannot be made by McDic's generation, then print $ 0 $ . In the second line, print all possible answers in ascending order, separated by spaces. If the given tree cannot be made by McDic's generation, then don't print anything.

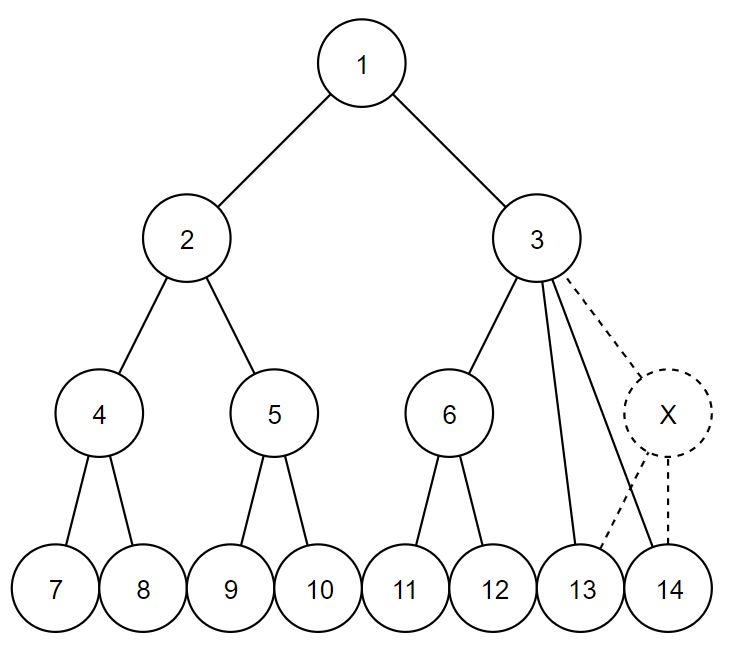In the first example, $ 3 $ is the only possible answer. In the second example, there are $ 2 $ possible answers. In the third example, the tree can't be generated by McDic's generation.