CF1228F One Node is Gone

给定一个正整数$n(2\le n\le17)$ 我们将会先生成一个大小为$2^n-1$的完全二叉树，其有一个根 现在以某种规则删去了其中的一个非根节点，具体规则如下： 设删去点为$u$ 那么我们会删去所有$u$的出边，然后将其所有直系儿子与$u$的父亲连一条边，特别的，如果$u$是一个叶子节点，则不会连边. 现在给定一棵树，希望你求出其能否以上述规则通过删除完全二叉树的一个点后得到，如果可以，求出方案数并输出所有方案中$u$的父亲，你需要升序输出

第一行一个正整数$n$ 接下来$2^n-3$行，每行描述给定树的一条边

第一行输出方案数，若不为$0$，则第二行升序输出所有可能的父亲节点，否则不输出第二行

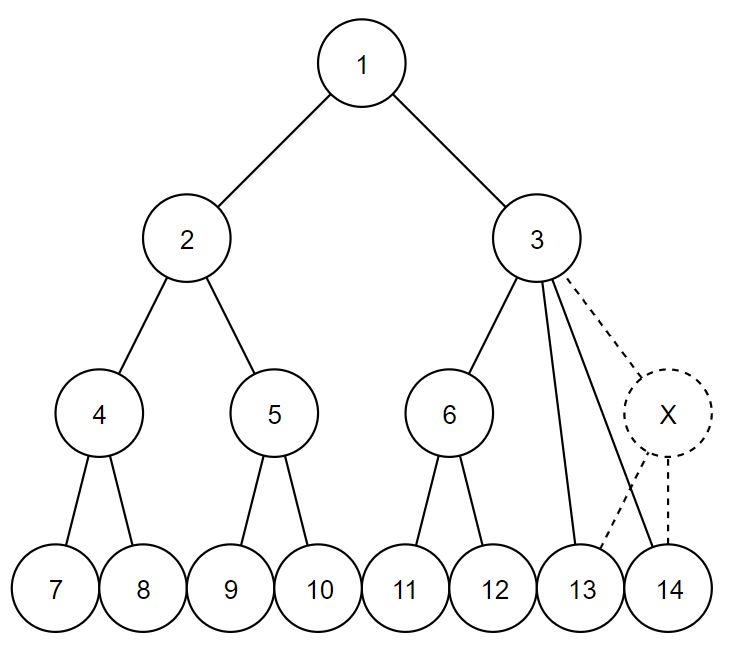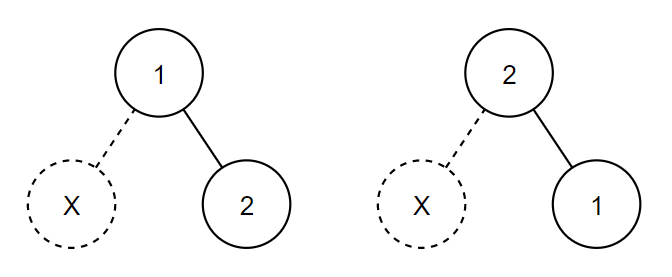In the first example, $ 3 $ is the only possible answer. In the second example, there are $ 2 $ possible answers. In the third example, the tree can't be generated by McDic's generation.