CF1234C Pipes

给你一个管道系统。该系统由两行组成，每行有 $n$ 个管道。左上角的管道坐标为 $(1, 1)$，右下角的管道坐标为 $(2, n)$。 共有六种类型的管道：两种直管和四种弯管。下图展示了所有六种类型的管道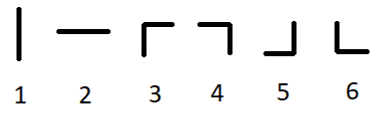：  管道类型 你可以将每个给定的管道顺时针或逆时针旋转 $90$ 度任意次（也可以不旋转），因此类型 $1$ 和 $2$ 可以互相变换，类型 $3, 4, 5, 6$ 也可以互相变换。 你希望通过旋转部分管道，使得水流可以从 $(1, 0)$（即左上角管道的左侧）进入，流入 $(1, 1)$ 处的管道，通过相连的管道流到 $(2, n)$ 处的管道，并最终流出到 $(2, n+1)$。 如果两个管道在系统中相邻且它们的端口相连，则认为它们是连通的。下图展示了一些连通的管道示例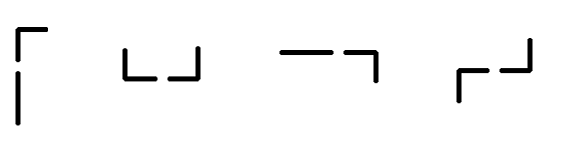：  连通管道示例 下面通过一个例子来说明问题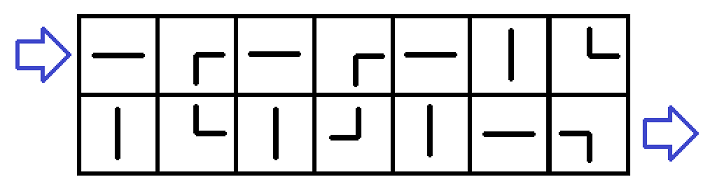：  第一个示例输入 其解答如下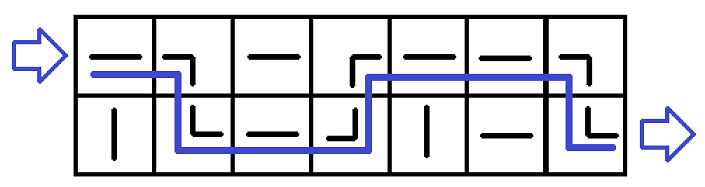：  第一个示例输出 如图所示，水流为蓝色曲线。为得到答案，需要将 $(1, 2)$ 处的管道顺时针旋转 $90$ 度，$(2, 3)$ 处的管道旋转 $90$ 度，$(1, 6)$ 处的管道旋转 $90$ 度，$(1, 7)$ 处的管道旋转 $180$ 度，$(2, 7)$ 处的管道旋转 $180$ 度。这样水流就可以从 $(1, 0)$ 流到 $(2, n+1)$。 你需要回答 $q$ 个独立的询问。

输入的第一行包含一个整数 $q$（$1 \le q \le 10^4$），表示询问的数量。接下来有 $q$ 个询问。 每个询问恰好包含三行。第一行为一个整数 $n$（$1 \le n \le 2 \times 10^5$），表示每行的管道数量。接下来的两行分别描述第一行和第二行的管道。每行由 $n$ 个数字组成，每个数字为 $1$ 到 $6$ 之间，表示该位置的管道类型。具体每个数字对应哪种管道请参见题目中的图片说明。 保证所有询问中 $n$ 的总和不超过 $2 \times 10^5$。

对于第 $i$ 个询问，输出一行答案，如果可以通过旋转部分管道使得水流从 $(1, 0)$ 流到 $(2, n+1)$，则输出 "YES"（不含引号），否则输出 "NO"。

样例中的第一个询问已在题目描述中给出。 由 ChatGPT 4.1 翻译