CF1237C2 Balanced Removals (Harder)

这是该问题的更难版本。在本版本中，$n \le 50\,000$。 在三维空间中有 $n$ 个互不相同的点，编号从 $1$ 到 $n$。第 $i$ 个点的坐标为 $(x_i, y_i, z_i)$。点的数量 $n$ 是偶数。 你需要通过一系列 $\frac{n}{2}$ 次“消除”操作移除所有 $n$ 个点。每次操作，你可以移除任意两个尚未被移除且构成“完全平衡对”的点 $a$ 和 $b$。如果不存在其他尚未被移除的点 $c$ 位于点 $a$ 和 $b$ 的轴对齐最小包围盒内，则点对 $a$ 和 $b$ 被称为“完全平衡对”。 形式化地说，若且唯若 $\min(x_a, x_b) \le x_c \le \max(x_a, x_b)$，$\min(y_a, y_b) \le y_c \le \max(y_a, y_b)$，且 $\min(z_a, z_b) \le z_c \le \max(z_a, z_b)$，则点 $c$ 位于点 $a$ 和 $b$ 的轴对齐最小包围盒内。注意，包围盒可能是退化的。 请找出一种方案，用 $\frac{n}{2}$ 次操作移除所有点。

第一行包含一个整数 $n$（$2 \le n \le 50\,000$，$n$ 为偶数），表示点的数量。 接下来的 $n$ 行，每行包含三个整数 $x_i, y_i, z_i$（$-10^8 \le x_i, y_i, z_i \le 10^8$），表示第 $i$ 个点的坐标。 任意两点不会重合。

输出 $\frac{n}{2}$ 行，每行两个整数 $a_i, b_i$（$1 \le a_i, b_i \le n$），表示第 $i$ 次操作中被移除的两个点的编号。每个 $1$ 到 $n$ 之间的整数恰好出现一次。 可以证明总是存在一种移除所有点的方案。如果有多种方案，输出任意一种即可。

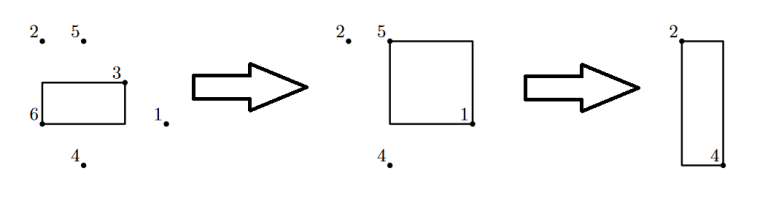
在第一个样例中，点及其对应的包围盒如下图所示（为简化起见，仅在 $z=0$ 平面上绘制）。注意，移除的顺序很重要：例如，点 $5$ 和 $1$ 最初并不能构成完全平衡对，但在点 $3$ 被移除后可以。  由 ChatGPT 4.1 翻译