CF1237E Balanced Binary Search Trees

回忆一下，二叉搜索树是一种有根二叉树，每个节点存储一个键值，并且每个节点最多有两个子树，分别为左子树和右子树。每个节点的键值必须大于其左子树中存储的所有键值，并且小于其右子树中存储的所有键值。 一个顶点的深度定义为从该顶点到根节点的简单路径上的边数。特别地，根节点的深度为 $0$。 我们称一棵二叉搜索树是“完全平衡”的，如果不存在另一棵具有相同顶点数的二叉搜索树，其所有顶点深度之和严格更小。 我们称一棵二叉搜索树为“条纹型”的，若对于每个顶点 $v$，都满足以下两个条件： - 如果 $v$ 有一个左子树，其根为 $u$，则 $v$ 的键值与 $u$ 的键值奇偶性不同。 - 如果 $v$ 有一个右子树，其根为 $w$，则 $v$ 的键值与 $w$ 的键值奇偶性相同。 给定一个整数 $n$，请你求出具有 $n$ 个顶点、键值为 $1$ 到 $n$ 且互不相同的“完全平衡条纹型二叉搜索树”的数量。请将答案对 $998\,244\,353$ 取模后输出。

输入仅包含一行，一个整数 $n$（$1 \le n \le 10^6$），表示需要的顶点数。

输出一个整数，表示具有 $n$ 个顶点、键值为 $1$ 到 $n$ 且互不相同的完全平衡条纹型二叉搜索树的数量，对 $998\,244\,353$ 取模。

在第一个样例中，只有如下这棵树满足所有条件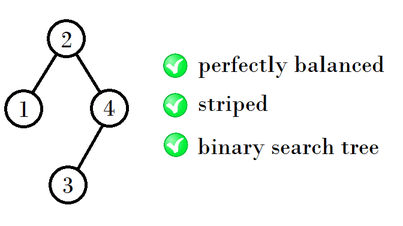： 在第二个样例中，下图中的各种树都不满足某些条件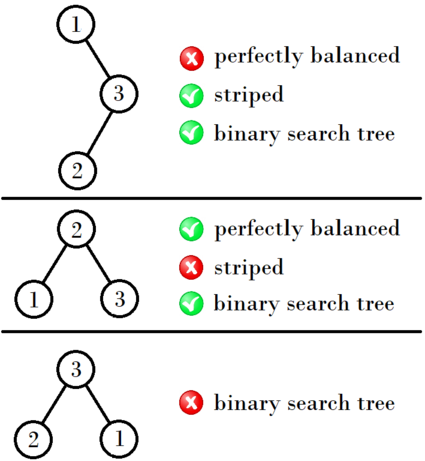： 由 ChatGPT 4.1 翻译