CF1237F Balanced Domino Placements

给定一个 $h$ 行 $w$ 列的方格棋盘，上面已经放置了一些多米诺骨牌。每个多米诺骨牌恰好覆盖棋盘上相邻的两个格子，每个格子最多只能被一个多米诺骨牌覆盖。 我们称一个多米诺骨牌的放置方式为“完全平衡”，如果没有任何一行或一列中存在被两个不同多米诺骨牌覆盖的两个格子。换句话说，每一行和每一列要么没有被覆盖的格子，要么只有一个被覆盖的格子，要么有两个被覆盖的格子且这两个格子属于同一个多米诺骨牌。 现在给定一个已经完全平衡的多米诺骨牌放置方式，问有多少种方法可以在此基础上再放置零个或多个多米诺骨牌，且仍然保持完全平衡。请输出方案数对 $998\,244\,353$ 取模的结果。

第一行包含三个整数 $h$、$w$ 和 $n$（$1 \le h, w \le 3600$，$0 \le n \le 2400$），分别表示棋盘的行数、列数和已经放置的多米诺骨牌数量。行编号从 $1$ 到 $h$，列编号从 $1$ 到 $w$。 接下来的 $n$ 行，每行包含四个整数 $r_{i,1}, c_{i,1}, r_{i,2}, c_{i,2}$（$1 \le r_{i,1} \le r_{i,2} \le h$，$1 \le c_{i,1} \le c_{i,2} \le w$），表示第 $i$ 个多米诺骨牌覆盖的两个格子的行号和列号。格子 $(r_{i,1}, c_{i,1})$ 和 $(r_{i,2}, c_{i,2})$ 是不同的，并且相邻。 给定的多米诺骨牌放置方式是完全平衡的。

输出在保持完全平衡的前提下，能够再放置零个或多个多米诺骨牌的方案数，对 $998\,244\,353$ 取模。

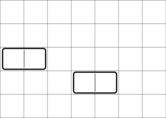
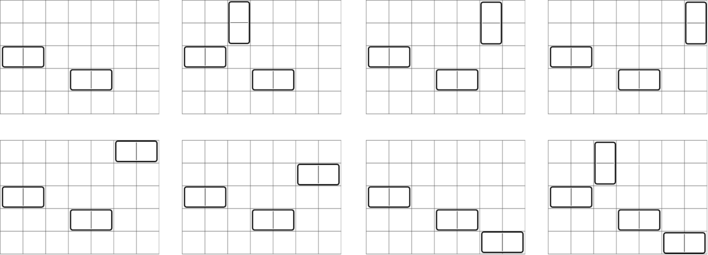
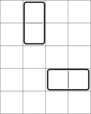
在第一个样例中，初始棋盘如下所示：  在这种情况下，有 $8$ 种方法可以在保持完全平衡的前提下放置零个或多个多米诺骨牌：  在第二个样例中，初始棋盘如下所示：  此时无法再放置任何多米诺骨牌。 由 ChatGPT 4.1 翻译