CF1238F The Maximum Subtree

Assume that you have $ k $ one-dimensional segments $ s_1, s_2, \dots s_k $ (each segment is denoted by two integers — its endpoints). Then you can build the following graph on these segments. The graph consists of $ k $ vertexes, and there is an edge between the $ i $ -th and the $ j $ -th vertexes ( $ i \neq j $ ) if and only if the segments $ s_i $ and $ s_j $ intersect (there exists at least one point that belongs to both of them). 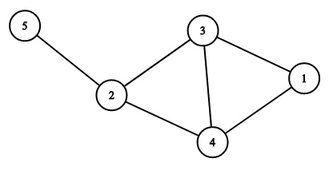For example, if $ s_1 = [1, 6], s_2 = [8, 20], s_3 = [4, 10], s_4 = [2, 13], s_5 = [17, 18] $ , then the resulting graph is the following: A tree of size $ m $ is good if it is possible to choose $ m $ one-dimensional segments so that the graph built on these segments coincides with this tree. You are given a tree, you have to find its good subtree with maximum possible size. Recall that a subtree is a connected subgraph of a tree. Note that you have to answer $ q $ independent queries.

The first line contains one integer $ q $ ( $ 1 \le q \le 15 \cdot 10^4 $ ) — the number of the queries. The first line of each query contains one integer $ n $ ( $ 2 \le n \le 3 \cdot 10^5 $ ) — the number of vertices in the tree. Each of the next $ n - 1 $ lines contains two integers $ x $ and $ y $ ( $ 1 \le x, y \le n $ ) denoting an edge between vertices $ x $ and $ y $ . It is guaranteed that the given graph is a tree. It is guaranteed that the sum of all $ n $ does not exceed $ 3 \cdot 10^5 $ .

For each query print one integer — the maximum size of a good subtree of the given tree.

In the first query there is a good subtree of size $ 8 $ . The vertices belonging to this subtree are $ {9, 4, 10, 2, 5, 1, 6, 3} $ .