CF1239A Ivan the Fool and the Probability Theory

最近，Ivan the Fool 决定变得更聪明，开始学习概率论。他认为自己已经相当理解这个学科，于是开始表现得像已经获得了该领域的博士学位一样。 为了证明自己的能力，Ivan 决定向朋友们展示“随机图片”的概念。一张图片是一个有 $n$ 行 $m$ 列的矩阵，每个格子要么是黑色，要么是白色。Ivan 认为，如果对于每个格子，至多只有一个相邻格子与它颜色相同，那么这张图片就是“随机”的。两个格子如果共享一条边，则被认为是相邻的。 Ivan 的兄弟们花了一些时间试图解释，这并不是通常意义上的随机。为了说服 Ivan，他们想要统计有多少种不同的“随机”图片（按照 Ivan 的定义）。如果两张图片中至少有一个格子的颜色不同，则认为它们是不同的。由于这样的图片数量可能非常大，请输出其对 $10^9 + 7$ 取模的结果。

一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 100\,000$），表示图片的行数和列数。

输出一个整数，表示“随机”图片的数量，对 $10^9 + 7$ 取模。

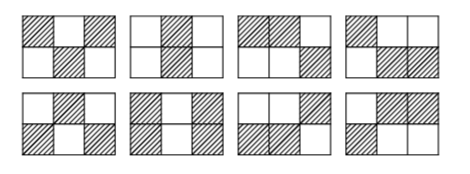
下图展示了所有 $2$ 行 $3$ 列的“随机”图片。  由 ChatGPT 4.1 翻译