CF123E Maze

一个迷宫由一棵树表示（无向图，任意两点之间恰好有一条路径）。在迷宫中，入口顶点和出口顶点以某种概率被选中。通过深度优先搜索（DFS）来寻找出口。如果有多种可行的移动方式，则等概率选择其中之一。伪代码如下： ```plain DFS(x) if x == exit vertex then finish search flag[x]

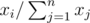
第一行给出图中顶点数 $n$（$1 \leq n \leq 10^{5}$）。接下来 $n-1$ 行，每行包含两个整数 $a_{i}$ 和 $b_{i}$，表示在顶点 $a_{i}$ 和 $b_{i}$ 之间存在一条边（$1 \leq a_{i}, b_{i} \leq n$）。保证给定的图是一棵树。 接下来的 $n$ 行，每行包含两个非负数 $x_{i}$ 和 $y_{i}$，分别表示选择第 $i$ 个顶点作为入口和出口的概率。选择第 $i$ 个顶点作为入口和出口的概率分别为  和 。 所有 $x_{i}$ 之和与所有 $y_{i}$ 之和均为正且不超过 $10^{6}$。

输出期望的移动步数。绝对误差或相对误差不超过 $10^{-9}$。

在第一个样例中，入口顶点始终为 1，出口顶点始终为 2。 在第二个样例中，入口顶点始终为 1，出口顶点以 $2/5$ 的概率为 2，以 $3/5$ 的概率为 3。对于出口顶点为 2 和 3 的情况，数学期望是相等的（对称情况）。第一次移动时，有 $0.5$ 的概率可以直接到达出口顶点，也有 $0.5$ 的概率到达不是出口顶点的顶点。在第一种情况下，移动步数为 1，在第二种情况下，移动步数为 3。总的数学期望为 $2/5 \times (1 \times 0.5 + 3 \times 0.5) + 3/5 \times (1 \times 0.5 + 3 \times 0.5)$。 由 ChatGPT 4.1 翻译