CF1240F Football
题目描述
世界上有 $n$ 个球队。
足球主席委员会(MFO)想主持最多 $m$ 场足球赛,MFO 希望第 $i$ 场比赛在球队 $a_i$ 和 $b_i$ 之间举办,举办场地为 $k$ 个体育场中的一个。
命名 $s_{i,j}$ 为第 $i$ 个队伍在第 $j$ 个体育场打的比赛的数量。MFO 不希望一个队伍在一个体育场打的比赛远多于在其他体育场打的比赛。所以,对于每一个队伍 $i$ ,其 $s_{i,1},s_{i,2},……,s_{i,k}$ 中,最大值和最小值的差的绝对值不应该超过 $2$。
每个队伍有一个 $w_i$ ,表示第 $i$ 个队伍每打一场比赛 MFO 赚取的收益。如果队伍 $i$ 打了 $l$ 场比赛,那么 MFO 将会获得 $w_i*l$ 的钱。
MFO 需要知道他们应该在哪个体育场举办哪一场比赛,使得在不违反他们设定的规则的前提下,赚取尽可能多的钱
然而这个问题对于 MFO 来说太复杂了,因此需要你的帮助。
输入格式
第一行包含三个整数 $n,m,k\ \ (3≤n≤100, 0≤m≤1000, 1≤k≤1000)$.
输出格式
对于每场比赛,输出 $t_i\ (1≤t_i≤k) $,表示这场比赛在第 $t_i$ 个体育场举行,如果第 $i$ 场比赛不应该被举办,则 $t_i=0$.
说明/提示
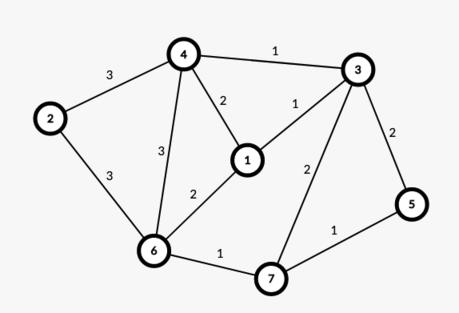
One of possible solutions to the example is shown below: