CF1242B 0-1 MST

Ujan 抽屉里有很多没用的东西，其中相当一部分是他的数学笔记本：是时候整理一下了。这一次他找到了一本旧的、落满灰尘的图论笔记本，上面描述了一个图。 这是一个有 $n$ 个顶点的无向带权图。它是一个完全图：每一对顶点之间都有一条边。每条边的权值要么为 $0$，要么为 $1$；恰好有 $m$ 条边的权值为 $1$，其余所有边的权值为 $0$。 由于 Ujan 并不想认真整理笔记，他决定求出该图的最小生成树的权值。（生成树的权值为其所有边权之和。）你能帮 Ujan 求出答案，让他不再拖延吗？

输入的第一行包含两个整数 $n$ 和 $m$（$1 \leq n \leq 10^5$，$0 \leq m \leq \min(\frac{n(n-1)}{2},10^5)$），分别表示顶点数和权值为 $1$ 的边的数量。 接下来的 $m$ 行中，第 $i$ 行包含两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$，$a_i \neq b_i$），表示第 $i$ 条权值为 $1$ 的边的两个端点。 保证输入中没有重复的边。

输出一个整数，表示该图的最小生成树的权值。

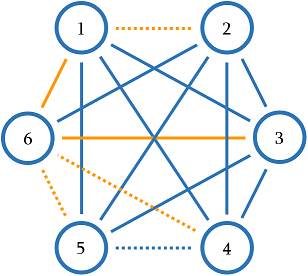
下图为第一个样例的图。虚线表示权值为 $0$ 的边，其他边权值为 $1$。其中一个最小生成树用橙色高亮，总权值为 $2$。  在第二个样例中，所有边的权值均为 $0$，因此任意生成树的总权值为 $0$。 由 ChatGPT 4.1 翻译