CF1242E Planar Perimeter

Ujan终于把他的房子打扫干净了，现在想装饰一下室内。他决定放置一块漂亮的地毯，将客房真正地连接起来。 他对多边形图块组成的地毯感兴趣，这样的图块的每一边要么是另一个（不同）图块的一边，要么是整个地毯外侧的一边。换句话说，地毯可以被表示为一个平面图，每个图块都对应于图的一面，每一面都是一个简单的多边形。地毯的周长就是图的外侧边的数量。 如果一个地毯由 $f$ 个图块组成，其中第 $i$ 个图块正好有 $a_{i}$ 条边，并且周长是最小的，那么Ujan认为它是美丽的。找到一个这样的地毯，这样Ujan就可以订购它了!

输入的第一行包含一个整数 $f$ ( $1 \le f \le 10^5$ )，表示地毯中图块的数量。 下一行包含 $f$ 个整数 $a_{1},...,a_{f}$ ( $3 \le a_{i} \le 3 \cdot 10^5 $，表示每个图块的边数。图块的边数 $a_{1} +...+ a_{f}$ 不会超过 $3 \cdot 10^5 $。

以图的形式输出地毯的描述 首先，输出一个整数 $n$ ( $3\le n\le 3\cdot 10^5$ ),表示图的节点数（节点必须从 $1$ 到 $n$ 编号）。 然后输出 $f$ 行，包含图的每一面的描述。第 $i$ 行应该描述第 $i$ 面，并且包含 $a_{i}$ 个不同的整数 $v_{i,1},...,v_{i,a_{i}}$ ( $1\le v_{i,j}\le n$ )，表示节点 $v_{i,j}$ 和节点 $v_{i,(j\mod a_{i})+1}$ 被任意一边连接。 该图应是平面的，并且满足问题描述中的限制，它的周长应该尽可能小。 **图中不应有重边或自环。** 图应是连通的。请注意，答案始终有解；如果有多个解，输出其中任何一个。

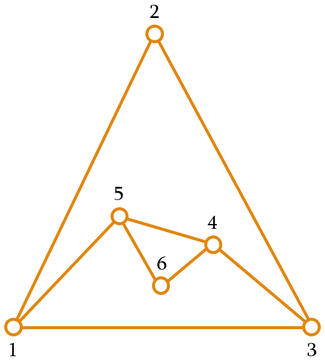
In the first sample, the two triangular faces are connected by a single edge, which results in the minimum perimeter $ 4 $ . The figure shows one possible configuration for the second sample. The minimum perimeter in this case is $ 3 $ .