CF1245D Shichikuji and Power Grid

Shichikuji 是南黑蜗牛寺的新任驻守神明。她的第一项工作如下： 在 X 县有 $n$ 个新城市。城市编号从 $1$ 到 $n$。第 $i$ 个城市位于距离神社北方 $x_i$ 千米、东面 $y_i$ 千米的位置。可能存在 $i \ne j$ 但 $(x_i, y_i) = (x_j, y_j)$ 的情况。 Shichikuji 必须为每个城市供电，可以通过在该城市建造发电站，或者将该城市与已经有电的城市连接来实现。也就是说，如果一个城市自身有发电站，或者通过直接连接或一系列连接与有电的城市相连，则该城市就有电。 - 在第 $i$ 个城市建造发电站的费用为 $c_i$ 日元； - 将第 $i$ 个城市与第 $j$ 个城市连接的费用为每千米 $(k_i + k_j)$ 日元。电线只能沿着正北、正南、正东、正西方向铺设，电线可以相互交叉。每根电线的两个端点都必须在某个城市。如果第 $i$ 个城市与第 $j$ 个城市连接，则电线会沿任意一条最短路径铺设。因此，连接第 $i$ 个城市与第 $j$ 个城市所需电线的长度为 $|x_i - x_j| + |y_i - y_j|$ 千米。 Shichikuji 希望以尽可能少的钱完成这项工作，因为在她看来，世界上除了钱什么都没有。然而，她小学五年级就去世了，所以她还不够聪明。因此，这位新任驻守神明向你寻求帮助。 你需要为 Shichikuji 提供以下信息：为所有城市供电所需的最小日元数、在哪些城市建造发电站，以及需要建立哪些连接。 如果存在多种选择城市和连接方式使得总花费最小，则输出任意一种即可。

输入的第一行包含一个整数 $n$（$1 \leq n \leq 2000$），表示城市的数量。 接下来 $n$ 行，每行包含两个用空格分隔的整数 $x_i$（$1 \leq x_i \leq 10^6$）和 $y_i$（$1 \leq y_i \leq 10^6$），表示第 $i$ 个城市的坐标。 下一行包含 $n$ 个用空格分隔的整数 $c_1, c_2, \dots, c_n$（$1 \leq c_i \leq 10^9$），表示在第 $i$ 个城市建造发电站的费用。 最后一行包含 $n$ 个用空格分隔的整数 $k_1, k_2, \dots, k_n$（$1 \leq k_i \leq 10^9$）。

第一行输出一个整数，表示为所有城市供电所需的最小日元数。 第二行输出一个整数 $v$，表示需要建造发电站的城市数量。 第三行输出 $v$ 个用空格分隔的整数，表示建造发电站的城市编号。每个编号应在 $1$ 到 $n$ 之间，且互不相同。编号顺序任意。 接下来一行输出一个整数 $e$，表示需要建立的连接数量。 最后输出 $e$ 行，每行包含两个整数 $a$ 和 $b$（$1 \leq a, b \leq n$，$a \ne b$），表示需要在城市 $a$ 和城市 $b$ 之间建立连接。每对无序城市对最多出现一次（即对于每个 $(a, b)$，不应有重复的 $(a, b)$ 或 $(b, a)$）。输出顺序任意。 如果存在多种选择城市和连接方式使得总花费最小，则输出任意一种即可。

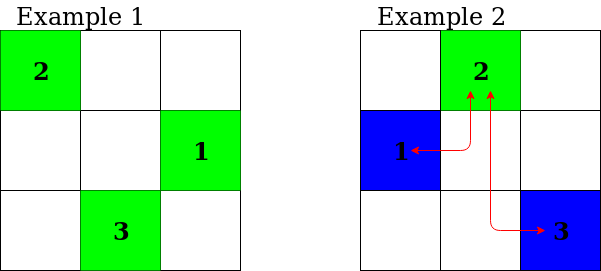
对于样例给出的答案，可参考下图（绿色为有发电站的城市，蓝色为其他城市，红色为电线）：  对于第一个样例，在所有城市建造发电站的总费用为 $3 + 2 + 3 = 8$。可以证明，没有任何方案的花费低于 8 日元。 对于第二个样例，在第 2 号城市建造发电站的费用为 2。连接城市 1 和城市 2 的费用为 $2 \cdot (3 + 2) = 10$。连接城市 2 和城市 3 的费用为 $3 \cdot (2 + 3) = 15$。因此总费用为 $2 + 10 + 15 = 27$。可以证明，没有任何方案的花费低于 27 日元。 由 ChatGPT 4.1 翻译