CF1245E Hyakugoku and Ladders

Hyakugoku 刚刚辞去了南黑蜗牛寺的常驻神明职位，决定追逐成为漫画家的梦想。她在那座寺庙里待了六个月，只是玩“翻绳”游戏，现在她想尝试另一种游戏——“蛇梯棋”。不幸的是，她已经把所有的蛇都杀掉了，所以现在只剩下梯子了。 游戏在一个 $10 \times 10$ 的棋盘上进行，规则如下： - 游戏开始时，玩家位于左下角的格子。 - 游戏的目标是让玩家沿着路径并通过垂直的梯子，最终到达终点（左上角的格子）。一旦玩家到达终点，游戏立即结束。 - 路径如下：如果某个格子不是本行的末尾，则它通向本行方向上的下一个格子；如果是本行的末尾，则通向正上方的格子。每一行的方向如下：最底下一行向右；其余每一行的方向与其下方一行相反。具体路径可参考提示部分的可视化图示。 - 每一回合，玩家掷一个标准六面骰子。假设骰子掷出的点数为 $r$。如果终点距离玩家当前位置不足 $r$ 格，则玩家不移动（但这回合仍然算作一次）。否则，玩家沿路径正好前进 $r$ 格并停下。如果玩家停在一个有梯子底端的格子上，可以选择是否爬上梯子。如果选择不爬，则下回合仍从该格子开始。 - 有些格子上有梯子。梯子只会垂直放置——每个梯子都通向上方某一行的同一列格子。玩家只有在掷骰子后停在梯子底端的格子上时，才能选择爬梯子。使用梯子后，玩家会直接到达梯子顶端的格子。爬梯子过程中不能中途离开。如果梯子顶端的格子同时也是另一个梯子的底端，玩家不能继续使用第二个梯子。 - 骰子的六个面分别为 1、2、3、4、5、6，每个点数出现的概率相同。 请注意： - 梯子可能重叠，但玩家在爬某个梯子时不能切换到其他梯子； - 梯子可以直接通到最顶行，但不能更高； - 可以有多个梯子通向同一个格子； - 梯子可以通向有其他梯子底端的格子，但如果玩家通过第一个梯子到达该格子，则不能再继续爬第二个梯子； - 玩家只能向上爬梯子，不能向下爬。 Hyakugoku 希望尽快完成游戏。因此，每一回合她都会最优地选择是否爬梯子。请你帮她计算完成游戏所需的最小期望回合数。

输入共十行。第 $i$ 行包含 10 个非负整数 $h_{i1}, h_{i2}, \dots, h_{i10}$。如果 $h_{ij}$ 为 $0$，则第 $i$ 行第 $j$ 列的格子没有梯子。否则，该格子的梯子高度为 $h_{ij}$，即爬上该梯子会到达正上方第 $h_{ij}$ 行的同一列格子。保证 $0 \leq h_{ij} < i$。此外，第一行第一个数和最后一行第一个数始终为 $0$，即终点和起始格子都没有梯子。

输出仅一行，一个浮点数，表示 Hyakugoku 最小期望完成游戏所需的回合数。若你的答案的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。

下图展示了路径和样例 2 的棋盘可视化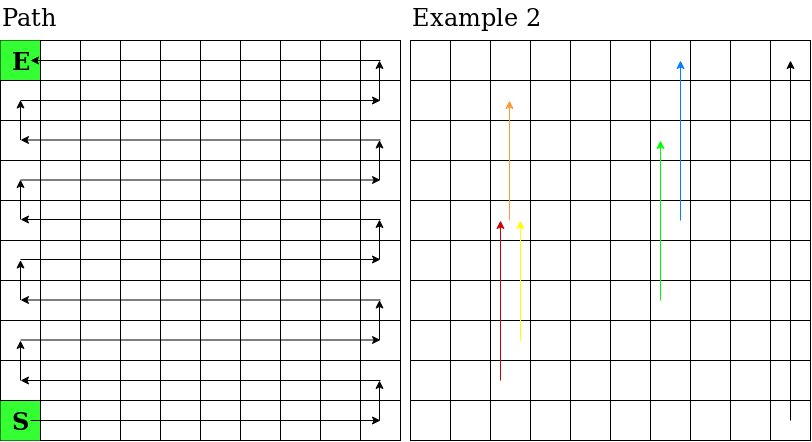： 标有 'S' 的格子为起始格，标有 'E' 的格子为终点。 对于第一个样例，没有任何梯子。 对于第二个样例，棋盘如右图所示（为便于区分，梯子已用不同颜色标出）。 梯子可能重叠，如红色和黄色梯子、绿色和蓝色梯子。梯子也可以直接通到最顶行，如黑色和蓝色梯子，但不能更高。也可能有多个梯子通向同一个格子，如红色和黄色梯子。此外，红色和黄色梯子都通向有橙色梯子的格子，因此如果玩家选择爬红色或黄色梯子，到达该格子后不能再继续爬橙色梯子。最后，绿色梯子经过了蓝色梯子的起点格子，但玩家在爬绿色梯子时不能切换到蓝色梯子。 由 ChatGPT 4.1 翻译