CF1250N Wires

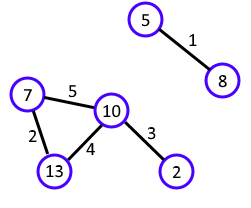
Polycarpus 有一个复杂的电子设备。该设备的核心是一块电路板。电路板上有 $10^9$ 个接触点，编号从 $1$ 到 $10^9$。此外，还有 $n$ 根编号为 $1$ 到 $n$ 的导线，每根导线连接电路板上的两个不同的接触点。若满足以下条件之一，则电信号可以在导线 $A$ 和 $B$ 之间传递： - 两根导线有相同的接触点； - 或者存在一系列导线，从 $A$ 开始到 $B$ 结束，且序列中每对相邻导线都共享一个接触点。  上图展示了一块有 $5$ 根导线的电路板。编号为 $2, 5, 7, 8, 10, 13$ 的接触点被使用。此时，电信号可以从第 $2$ 根导线传递到第 $3$ 根导线，但无法传递到第 $1$ 根导线。 目前电路板损坏了。Polycarpus 认为，如果能重新焊接导线，使得任意两根导线之间都能传递信号，电路板就能修好。 Polycarpus 重新焊接一根导线的一端需要 $1$ 分钟。也就是说，改变一根导线的一个接触点需要 $1$ 分钟。可以将任意一个接触点更换为区间 $[1, 10^9]$ 内的任意接触点。每根导线的两端必须始终连接到不同的接触点。两端都重新焊接需要两次操作，总共 $2$ 分钟。 请你计算，Polycarpus 至少需要多少分钟才能重新焊接导线，使得任意两根导线之间都能传递信号。并输出一种最优的焊接操作序列。

输入包含一个或多个测试用例。第一行包含一个整数 $t$，表示测试用例的数量。接下来是 $t$ 个测试用例。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^5$），表示导线的数量。接下来的 $n$ 行，每行包含两个用空格分隔的整数 $x_i, y_i$（$1 \le x_i, y_i \le 10^9$，$x_i \neq y_i$），表示第 $i$ 根导线连接的两个接触点。两根导线可以连接同一对接触点。 所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，首先输出一行一个整数 $k$，表示最少需要重新焊接的次数。接下来的 $k$ 行，每行输出三个整数 $w_j, a_j, b_j$（$1 \le w_j \le n$，$1 \le a_j, b_j \le 10^9$）。表示在第 $j$ 次焊接操作中，将第 $w_j$ 根导线原本连接的 $a_j$ 号接触点改为连接 $b_j$ 号接触点。每次焊接后，导线必须连接两个不同的接触点。如果有多种最优方案，输出任意一种即可。

由 ChatGPT 4.1 翻译