CF1251F Red-White Fence

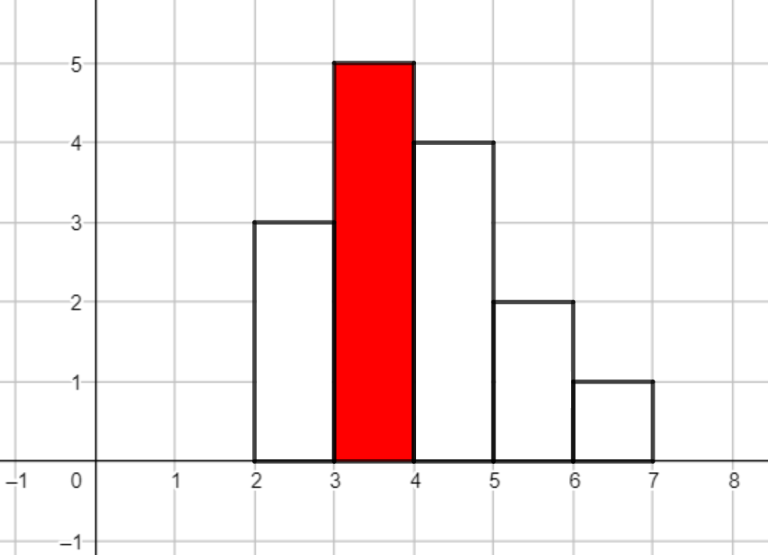
Polycarp想在他家附近建一道栅栏。他有$n$个白板和$k$个红板去建造它。每一块板都有一个整数长度。 一个好的栅栏应由一块红板和几块（可能是零块）白板组成。红色的板应该在这道栅栏中是**最长的**，而且红板前的板子长度应为递增，而红板之后的板子长度为递减。如果用了$m$块板子，它们的长度从左到右依次是$l_1,l_2,…,l_m$，那么应该符合以下条件 ①栅栏上应**有且只有一块**红板，设其序号为$j$ ②对于所有的$i∈[1,j-1]$有$l_il_{i+1}$ 在Polycarp建造他的栅栏时，他会从左向右在$0$高度上放置所有板，没有间隙，所以这些板将会组成一个多边形：  例图：一个栅栏的板长数组为$[3,5,4,2,1]$，第二个板是红板。栅栏的周长是$20$。Polycrp对一些特殊周长的栅栏感兴趣。他有喜欢的$q$个偶整数$[Q_1,Q_2,…,Q_q]$，对于每个这样的整数$Q_i$，他想计算有几种不同的周长是$Q_i$的篱笆可以被造出来（如果两个篱笆的板长排列不同，那么就认为这两个篱笆是不同的）你可以帮他计算这些数值吗？

输入第一行是两个正整数$n,k(1≤n≤3*10^5,1≤k≤5)$，表示Polycarp拥有的白板和红板的数量 第二行有$n$个正整数$[a_1,a_2,...,a_n](1≤a_i≤3*10^5)$，表示Polycarp拥有的$n$块白板的长度 第三行有$k$个正整数$[b_1,b_2,...,b_k](1≤b_i≤3*10^5)$，表示Polycarp拥有的$k$块红板的长度，所有$b_i$都是不相同的 第四行是一个正整数$q(1≤q≤3*10^5)$，表示特殊周长的数量 第五行有$q$个正整数$[Q_1,Q_2,...,Q_q](4≤Q_i≤12*10^5)$，每个$Q_i$都是偶数，表示Polycarp喜欢的特殊整数（即特殊周长）

对于每个$Q_i$，输出一个整数，表示有多少种符合约束条件的周长为$Q_i$的栅栏，由于数量可能很大，结果请对$998244353$取模，每个输出占一行

对于第一个样例，可能的长度序列有（红板加粗） ·周长为$6$：$[$**2**$]$ ·周长为$8$：$[1,$ **2**$]$,$[$**2**$,1]$ ·周长为$10$：$[1,$ **2**$,1]$,$[$**4**$]$ ·周长为$12$：$[1,$ **4**$]$,$[3,$ **4**$]$,$[$**4**$,1]$,$[$**4**$,3]$ ·周长为$14$：$[1,$ **4**$,1]$,$[1,$ **4**$,3]$,$[3,$ **4**$,1]$,$[3,$ **4**$,3]$,$[1,3,$ **4**$]$,$[$**4**$,3,1]$ ·周长为$16$：$[1,$ **4**$,3,1]$,$[3,$ **4**$,3,1]$,$[1,3,$ **4**$,1]$,$[1,3,$ **4**$,3]$ ·周长为$18$：$[1,3,$ **4**$,3,1]$