CF1252C Even Path

路径查找是寻找两点之间路线的任务，在许多问题中经常出现。例如，在 GPS 导航软件中，驾驶员可以查询建议路线；在机器人运动规划中，需要找到一系列有效的动作来完成某些任务；或者在简单的迷宫求解器中，需要找到从一个点到另一个点的有效路径。本题与迷宫求解有关。 本题中考虑的迷宫是一个 $N \times N$ 的整数矩阵 $A$。每个格子的值由给定的两个长度为 $N$ 的整数数组 $R$ 和 $C$ 生成。具体地，第 $i$ 行第 $j$ 列的格子 $(i,j)$ 的值等于 $R_i + C_j$。注意，本题中所有的下标均从 $1$ 到 $N$。 在这个迷宫中，一条路径被定义为一系列格子 $(r_1,c_1), (r_2,c_2), \dots, (r_k,c_k)$，满足对于所有 $1 \le i < k$，都有 $|r_i - r_{i+1}| + |c_i - c_{i+1}| = 1$。换句话说，相邻的两个格子只能在行或列上相差 $1$。在本题中，一条“偶数路径”被定义为路径上所有格子的值都是偶数的路径。 给定一个四元组 $\langle r_a, c_a, r_b, c_b \rangle$ 作为一次询问，你的任务是判断是否存在一条偶数路径，从格子 $(r_a, c_a)$ 到格子 $(r_b, c_b)$。为简化问题，保证 $(r_a, c_a)$ 和 $(r_b, c_b)$ 这两个格子的值都是偶数。 例如，设 $N = 5$，$R = \{6, 2, 7, 8, 3\}$，$C = \{3, 4, 8, 5, 1\}$。下图展示了由给定数组 $R$ 和 $C$ 生成的 $5 \times 5$ 的矩阵 $A$。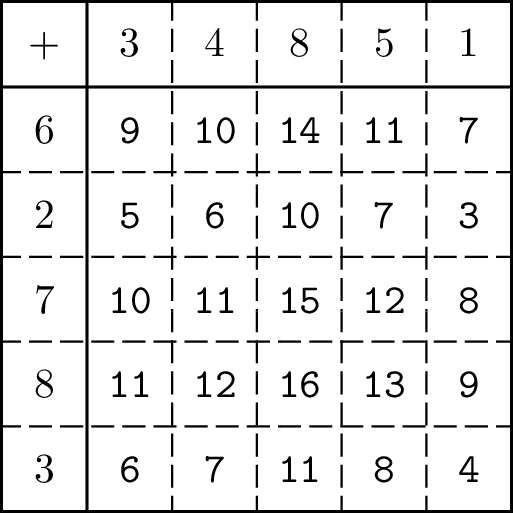  我们来看几个询问： - $\langle 2, 2, 1, 3 \rangle$：存在一条偶数路径从格子 $(2,2)$ 到格子 $(1,3)$，例如 $(2,2), (2,3), (1,3)$。当然，$(2,2), (1,2), (1,3)$ 也是一条有效的偶数路径。 - $\langle 4, 2, 4, 3 \rangle$：存在一条偶数路径从格子 $(4,2)$ 到格子 $(4,3)$，即 $(4,2), (4,3)$。 - $\langle 5, 1, 3, 4 \rangle$：不存在偶数路径从格子 $(5,1)$ 到格子 $(3,4)$。可以观察到，$(5,1)$ 的两个相邻格子分别是 $(5,2)$ 和 $(4,1)$，它们的值都是奇数（7 和 11），因此无法从 $(5,1)$ 出发形成任何偶数路径。

输入的第一行包含两个整数 $N$ 和 $Q$（$2 \le N \le 100\,000$，$1 \le Q \le 100\,000$），分别表示迷宫的大小和询问的数量。接下来一行包含 $N$ 个整数 $R_i$（$0 \le R_i \le 10^6$），表示数组 $R$。再下一行包含 $N$ 个整数 $C_i$（$0 \le C_i \le 10^6$），表示数组 $C$。接下来的 $Q$ 行，每行包含四个整数 $r_a$、$c_a$、$r_b$、$c_b$（$1 \le r_a, c_a, r_b, c_b \le N$），表示一次询问 $\langle r_a, c_a, r_b, c_b \rangle$。保证 $(r_a, c_a)$ 和 $(r_b, c_b)$ 是迷宫中的两个不同格子，且它们的值都是偶数。

对于每个询问，按输入顺序输出一行，内容为字符串 "YES"（不带引号）或 "NO"（不带引号），表示是否存在一条偶数路径从格子 $(r_a, c_a)$ 到格子 $(r_b, c_b)$。

样例输入输出 #1 的说明 这就是题目描述中的示例。 由 ChatGPT 4.1 翻译