CF1252F Regular Forestation

造林通常指的是种植大量树木以形成森林，通常用于替代被砍伐的森林。然而，图论学家却有另一种“造林”的方式——通过砍掉一棵树！ 一棵树是一个包含 $N$ 个节点、$N-1$ 条边的连通无环图。设 $U$ 是一棵树，$u$ 是树 $U$ 中的一个节点，且 $u$ 的度数至少为 $2$（即 $u$ 至少与 $2$ 个其他节点直接相连）。如果我们从 $U$ 中移除 $u$，那么会得到两个或更多不连通的（更小的）树，这在图论中被称为森林。在本题中，我们将研究图论学家所定义的特殊“造林”方式。 设 $V(S)$ 表示树 $S$ 的节点集合，$V(T)$ 表示树 $T$ 的节点集合。如果存在一个双射 $f : V(S) \rightarrow V(T)$，使得对于 $V(S)$ 中任意一对节点 $(s_i, s_j)$，当且仅当 $s_i$ 和 $s_j$ 在 $S$ 中有边相连时，$f(s_i)$ 和 $f(s_j)$ 在 $T$ 中也有边相连，则称树 $S$ 和树 $T$ 是同构的。注意，$f(s) = t$ 意味着 $S$ 中的节点 $s$ 与 $T$ 中的节点 $t$ 一一对应。 我们称树 $U$ 中的一个节点 $u$ 为“良好切割点”，当且仅当移除 $u$ 后，$U$ 被分成两个或更多不连通的树，且这些树两两同构。 给定一棵树 $U$，你的任务是判断 $U$ 中是否存在良好切割点。如果存在，输出通过移除一个良好切割点所能得到的不连通树的最大数量；如果不存在，输出 $-1$。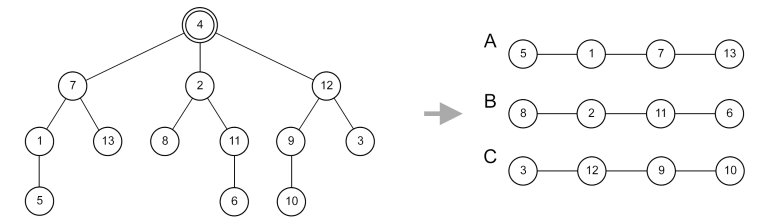 例如，考虑下图所示的 $13$ 个节点的树：  这棵树中恰好有一个良好切割点，即节点 $4$。注意，移除节点 $4$ 后，会得到三棵同构的树（在本例中为链式结构），分别为 $\{5, 1, 7, 13\}$、$\{8, 2, 11, 6\}$ 和 $\{3, 12, 9, 10\}$，在图中分别用 $A$、$B$、$C$ 表示。 - $A$ 与 $B$ 之间的双射函数：$f(5) = 8$，$f(1) = 2$，$f(7) = 11$，$f(13) = 6$。 - $A$ 与 $C$ 之间的双射函数：$f(5) = 3$，$f(1) = 12$，$f(7) = 9$，$f(13) = 10$。 - $B$ 与 $C$ 之间的双射函数：$f(8) = 3$，$f(2) = 12$，$f(11) = 9$，$f(6) = 10$。 当然，这些树之间还存在其他的双射函数。

输入的第一行包含一个整数 $N$（$3 \le N \le 4000$），表示给定树的节点数。接下来的 $N-1$ 行，每行包含两个整数 $a_i$、$b_i$（$1 \le a_i < b_i \le N$），表示树中的一条边 $(a_i, b_i)$。保证给定的图是一棵树，即任意两节点之间都存在一条路径。

输出一行一个整数，表示通过移除一个良好切割点所能得到的不连通树的最大数量。如果不存在良好切割点，输出 $-1$。

样例输入输出 #1 的说明 这正是题目描述中的示例。 由 ChatGPT 4.1 翻译