CF1252I Mission Possible

Allen 是一名政府特工，他的任务是潜入一个黑帮的秘密基地，获取有关黑帮活动的重要情报。 这个秘密基地是一个矩形区域，以笛卡尔坐标系中的点 $(x_L, y_L)$、$(x_L, y_R)$、$(x_R, y_L)$ 和 $(x_R, y_R)$ 定义，其中 $x_L < x_R$ 而且 $y_L < y_R$。基地内部有 $N$ 个传感器。每个传感器 $i$ 位于坐标 $(x_i, y_i)$，其有效探测半径为 $r_i$，能够检测到距离 $(x_i, y_i)$ 严格小于 $r_i$ 的任何人。换句话说，传感器 $i$ 只有在两者的欧几里得距离严格小于 $r_i$ 时才能探测到位于 $(x_a, y_a)$ 位置的人。此外，任意两个传感器 $i$ 和 $j$ 的间距都严格大于 $r_i + r_j$。需要牢记，两点 $(x_a, y_a)$ 和 $(x_b, y_b)$ 之间的欧几里得距离为 $\sqrt{|x_a - x_b|^2 + |y_a - y_b|^2}$。 Allen 将从位置 $(x_s, y_s)$ 开始渗透，目标位置为 $(x_t, y_t)$。他能够在直线方向上飞奔，但改变方向时需要额外时间。尽管速度飞快，他必须确保在跑步过程中不被任何传感器探测到，即奔跑路径上任何点都不能处于传感器的有效探测范围内。 设 $P = \{(x_{p_1}, y_{p_1}), \dots, (x_{p_{|P|}}, y_{p_{|P|}})\}$ 为 Allen 改变路线的节点集合。那么 Allen 的奔跑路线为 $(x_s, y_s) \rightarrow (x_{p_1}, y_{p_1}) \rightarrow \dots \rightarrow (x_{p_{|P|}}, y_{p_{|P|}}) \rightarrow (x_t, y_t)$。其中，$(x_a, y_a) \rightarrow (x_b, y_b)$ 表示 Allen 在这段路径上直线奔跑。集合 $P$ 是可行的，当且仅当选择该 $P$ 时，Allen 在不被任何传感器探测到的情况下没有跑出秘密基地（不过 Allen 可以沿着基地的边界跑）。需要注意的是，$P$ 中的$x_p$和$y_p$可以是实数，不一定是整数。 你的任务是找到一个可行的 $P$，其中最多包含 1000 个点。

输入的第一行包含五个整数：$N$ $x_L$ $y_L$ $x_R$ $y_R$，表示传感器的数量和秘密基地矩形的四个边界（$0 \le N \le 50$；$0 \le x_L < x_R \le 1000$；$0 \le y_L < y_R \le 1000$）。接下来的一行是两整数：$x_s$ $y_s$，表示 Allen 的初始位置（$x_L < x_s < x_R$；$y_L < y_s < y_R$）。然后再给出两整数：$x_t$ $y_t$，表示 Allen 的目标位置（$x_L < x_t < x_R$；$y_L < y_t < y_R$），保证 $x_s \ne x_t$ 或 $y_s \ne y_t$。接下来的 $N$ 行中每行包含三个整数：$x_i$ $y_i$ $r_i$，表示一个传感器的位置 $(x_i, y_i)$ 和它的探测半径 $r_i$（$x_L < x_i - r_i < x_i + r_i < x_R$；$y_L < y_i - r_i < y_i + r_i < y_R$；$1 \le r_i \le 1000$）。保证任意两传感器之间的欧几里得距离都大于 $r_i + r_j$。同时保证初始位置 $(x_s, y_s)$ 和目标位置 $(x_t, y_t)$ 到任意传感器 $i$ 的距离都大于 $r_i$。

首先输出一个整数，表示可行 $P$ 中的路径节点数。随后在接下来的 $|P|$ 行中，每行输出两个实数（以单个空格分隔）；第 $j$ 行表示 $P$ 中的第 $j$ 个节点 $x_j$ $y_j$。你可以输出任何一个满足条件的可行 $P$，但点数不能超过 1000 个。 由于输出涉及浮点数，我们定义一个误差值 $\epsilon$ 为 $10^{-6}$ 以验证输出的正确性。令 $Q_1 = (x_s, y_s)$，$Q_{j+1} = P_j$，对于所有 $1 \le j \le |P|$，以及 $Q_{|P|+2} = (x_t, y_t)$。则 $P$ 被视为正确如果且仅如果满足以下条件： - 对于所有 $1 \le k \le |P|$，有 $x_L - \epsilon \le x_{p_k} \le x_R + \epsilon$ 且 $y_L - \epsilon \le y_{p_k} \le y_R + \epsilon$（Allen 没有跑出秘密基地）。 - 对于所有 $1 \le k < |Q|$，设 $S_k$ 为连接 $Q_k$ 和 $Q_{k+1}$ 的线段（Allen 在直线上奔跑）。对于所有 $1 \le i \le N$，设 $(x_{k,i}, y_{k,i})$ 为 $S_k$ 上距离第 $i$ 个传感器位置 $(x_i, y_i)$ 最近的点。设 $d_{k,i}$ 为 $(x_{k,i}, y_{k,i})$ 和 $(x_i, y_i)$ 之间的距离。应满足约束 $r_i \le d_{k,i} + \epsilon$（Allen 没有被任何传感器探测到）。 - $Q$ 中的所有点都是不同的。即两点 $(x_a, y_a)$ 和 $(x_b, y_b)$ 只有在 $|x_a - x_b| > \epsilon$ 或 $|y_a - y_b| > \epsilon$ 时才被视为不同。 **本翻译由 AI 自动生成**

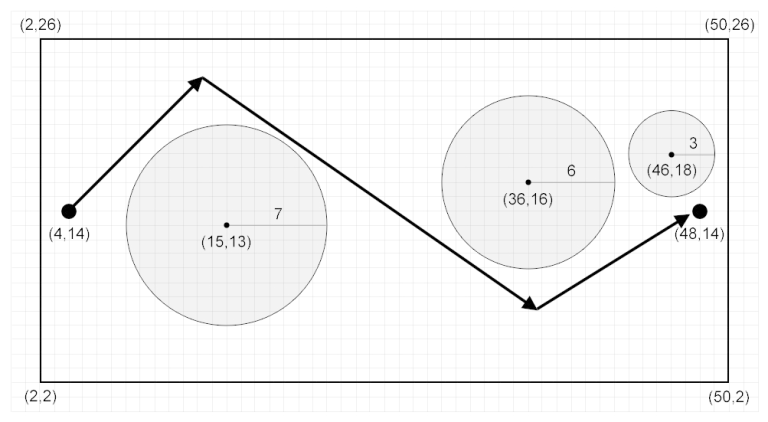
Explanation for the sample input/output #1  The figure above shows the $ P $ from the sample output. Note that there exists a feasible $ P $ with only one point in this sample, although you are not required to find such $ P $ .