CF1254D Tree Queries

Hanh 是一位著名的生物学家。他喜欢在自己的花园里种树并做实验。 有一天，他得到了一棵包含 $n$ 个顶点的树。顶点编号为 $1$ 到 $n$。一棵有 $n$ 个顶点的树是一个无向连通图，包含 $n-1$ 条边。最初，Hanh 将每个顶点的值都设为 $0$。 现在，Hanh 要进行 $q$ 次操作，每次操作有以下两种类型之一： - 类型 $1$：Hanh 选择一个顶点 $v$ 和一个整数 $d$。然后他随机均匀地选择一个顶点 $r$，列出所有从 $r$ 到 $u$ 的路径经过 $v$ 的顶点 $u$。Hanh 将所有这样的顶点 $u$ 的值增加 $d$。 - 类型 $2$：Hanh 选择一个顶点 $v$，并计算 $v$ 的期望值。 由于 Hanh 擅长生物学但不擅长数学，他需要你来帮助完成这些操作。

第一行包含两个整数 $n$ 和 $q$（$1 \leq n, q \leq 150\,000$），分别表示 Hanh 的树的顶点数和他要进行的操作数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$），表示存在一条连接顶点 $u$ 和 $v$ 的边。保证这 $n-1$ 条边构成一棵树。 最后 $q$ 行，每行描述一次操作，格式如下： - $1\ v\ d$（$1 \leq v \leq n, 0 \leq d \leq 10^7$），表示一次第一类操作。 - $2\ v$（$1 \leq v \leq n$），表示一次第二类操作。 保证至少有一次第二类操作。

对于每一次第二类操作，输出一行该顶点的期望值。 设 $M = 998244353$，可以证明，期望值可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数且 $q \not\equiv 0 \pmod{M}$。输出满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$ 的整数 $x$。

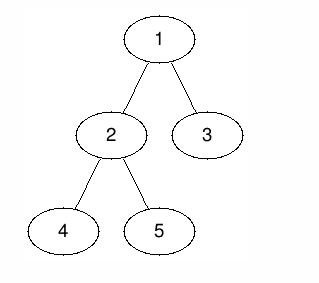
下图展示了样例中的树结构：  对于第一个查询，$v = 1$ 且 $d = 1$： - 若 $r = 1$，所有顶点的值都增加。 - 若 $r = 2$，顶点 $1$ 和 $3$ 的值增加。 - 若 $r = 3$，顶点 $1$、$2$、$4$ 和 $5$ 的值增加。 - 若 $r = 4$，顶点 $1$ 和 $3$ 的值增加。 - 若 $r = 5$，顶点 $1$ 和 $3$ 的值增加。 因此，这次操作后所有顶点的期望值为（$1, 0.4, 0.8, 0.4, 0.4$）。 对于第二个查询，$v = 2$ 且 $d = 2$： - 若 $r = 1$，顶点 $2$、$4$ 和 $5$ 的值增加。 - 若 $r = 2$，所有顶点的值都增加。 - 若 $r = 3$，顶点 $2$、$4$ 和 $5$ 的值增加。 - 若 $r = 4$，顶点 $1$、$2$、$3$ 和 $5$ 的值增加。 - 若 $r = 5$，顶点 $1$、$2$、$3$ 和 $4$ 的值增加。 因此，这次操作后所有顶点的期望值为（$2.2, 2.4, 2, 2, 2$）。 由 ChatGPT 4.1 翻译