CF1263F Economic Difficulties

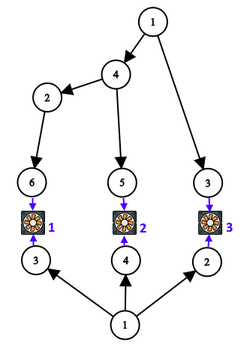
Berland 宫殿的电网由两套系统组成：主电网和备用电网。宫殿中的电线由昂贵的材料制成，因此出售其中一些电线是个不错的主意！ 每个电网（主电网和备用电网）都有一个首节点（编号为 $1$）。每个其他节点都从首节点获得电力。每个节点都可以通过唯一的一条路径从首节点到达。此外，每个电网恰好有 $n$ 个节点，这些节点不再向下分配电力。 换句话说，每个电网都是一棵以 $1$ 号节点为根的有向树，且有 $n$ 个叶子节点。每棵树的节点编号独立，且两棵树之间的节点没有连接。 此外，宫殿里有 $n$ 台电器。每台电器都连接到主电网的一个节点和备用电网的一个节点。电器只连接到那些不再向下分配电力的节点（即树的叶子）。每个电网的每个叶子节点都恰好连接一台电器。  在这个例子中，主电网包含 $6$ 个节点（上方的树），备用电网包含 $4$ 个节点（下方的树）。有 $3$ 台电器，编号用蓝色标出。 保证整个电网（两套电网和 $n$ 台电器）都可以如上图所示地表示： - 主电网是上方的树，电线方向为“自上而下”； - 备用电网是下方的树，电线方向为“自下而上”； - 电器位于两套电网之间的一排，编号从 $1$ 到 $n$，从左到右排列； - 两套电网内部的连线不会相交。 形式化地说，对于每棵树，都存在一次从 $1$ 号节点出发的深度优先遍历，遍历叶子的顺序与电器 $1,2,\dots,n$ 的连接顺序一致（首先访问连接到电器 $1$ 的节点，然后是电器 $2$，依此类推）。 商人希望尽可能多地出售（移除）电线，同时保证每台电器至少能从一套电网（主电网或备用电网）获得电力。换句话说，对于每台电器，至少存在一条仅包含同一电网节点的路径，从该电器连接的节点到首节点。

第一行包含一个整数 $n$（$1 \le n \le 1000$），表示宫殿中的电器数量。 第二行包含一个整数 $a$（$1 + n \le a \le 1000 + n$），表示主电网的节点数。 第三行包含 $a-1$ 个整数 $p_i$（$1 \le p_i \le a$）。每个 $p_i$ 表示主电网中存在一条从 $p_i$ 号节点到第 $i+1$ 号节点的电线。 第四行包含 $n$ 个整数 $x_i$（$1 \le x_i \le a$），表示第 $i$ 台电器连接的主电网节点编号。 第五行包含一个整数 $b$（$1 + n \le b \le 1000 + n$），表示备用电网的节点数。 第六行包含 $b-1$ 个整数 $q_i$（$1 \le q_i \le b$）。每个 $q_i$ 表示备用电网中存在一条从 $q_i$ 号节点到第 $i+1$ 号节点的电线。 第七行包含 $n$ 个整数 $y_i$（$1 \le y_i \le b$），表示第 $i$ 台电器连接的备用电网节点编号。 保证每个电网都是一棵有 $n$ 个叶子的树，且每个叶子节点都连接一台电器。同时保证对于每棵树，都存在一次从 $1$ 号节点出发的深度优先遍历，遍历叶子的顺序与电器的连接顺序一致。

输出一个整数，表示在保证每台电器都能通电的前提下，最多可以切断多少根电线。

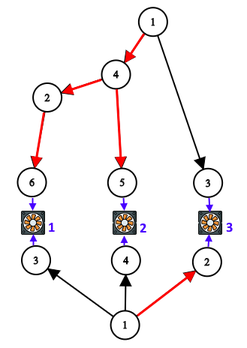
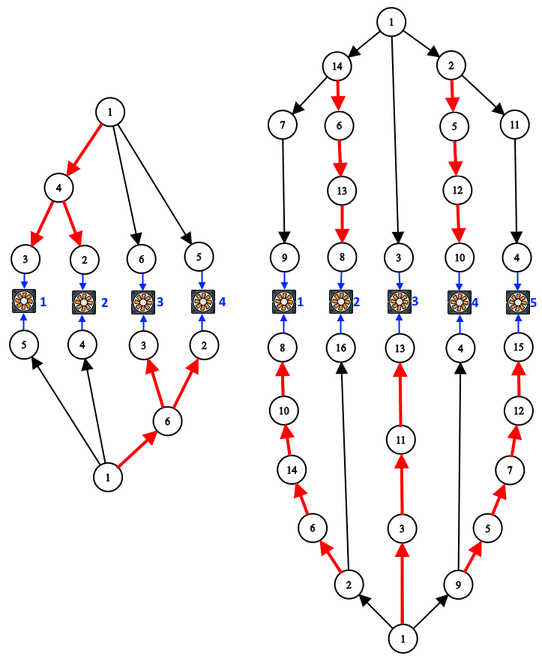
对于第一个样例，下图展示了一种可能的方案（红色标记的为可移除的电线）：  第二个和第三个样例如下图所示：  由 ChatGPT 4.1 翻译