CF1266H Red-Blue Graph

有一个有向图，包含 $n$ 个顶点，编号为 $1$ 到 $n$，其中每个顶点（除了 $n$ 号顶点）都有两条出边，分别为红色和蓝色。任意时刻，每个顶点恰好有一条出边处于激活状态。初始时，所有蓝色边处于激活状态，并且有一个标记位于顶点 $1$。每经过一秒，标记所在的顶点会首先切换其激活的出边——未激活的边变为激活，原本激活的边变为未激活。然后，标记沿着当前激活的出边移动。当标记到达顶点 $n$ 时，过程停止。保证从任意顶点都可以通过若干条边到达顶点 $n$。 你将得到 $q$ 个询问。每个询问包含一个图的状态——一个形如 $(v, s)$ 的二元组，其中： - $v$ 表示当前标记所在的顶点； - $s$ 是一个长度为 $n-1$ 的字符串，第 $i$ 个字符表示第 $i$ 个顶点当前激活的出边颜色（若为红色则为 'R'，否则为 'B'）。 对于每个询问，判断该状态是否可以从初始状态经过若干步到达，并输出该状态第一次出现的时刻。注意，切换激活边和沿边移动这两个操作是原子的——如果某个状态只在切换激活边后、移动前出现，则不认为到达了该状态。

第一行包含一个整数 $n$（$2 \leq n \leq 58$），表示顶点数。 接下来 $n-1$ 行，第 $i$ 行包含两个用空格分隔的整数 $b_i$ 和 $r_i$（$1 \leq b_i, r_i \leq n$），分别表示从 $i$ 号顶点出发的蓝色边 $(i, b_i)$ 和红色边 $(i, r_i)$。保证从任意顶点都可以到达顶点 $n$。 接下来一行包含一个整数 $q$（$1 \leq q \leq 5000$），表示询问数。 接下来 $q$ 行，每行包含一个整数 $v$（$1 \leq v < n$）和一个长度为 $n-1$ 的字符串 $s$，仅由 'R' 和 'B' 组成。第 $i$ 个字符为 'R' 表示第 $i$ 个顶点的红色边处于激活状态，否则为 'B'。

输出 $q$ 行，每行对应一个询问的答案。 如果第 $i$ 个询问中的状态无法到达，输出 $-1$。否则，输出 $t_i$，即该状态第一次出现的时刻（从初始状态算起，初始状态为第 $0$ 秒）。

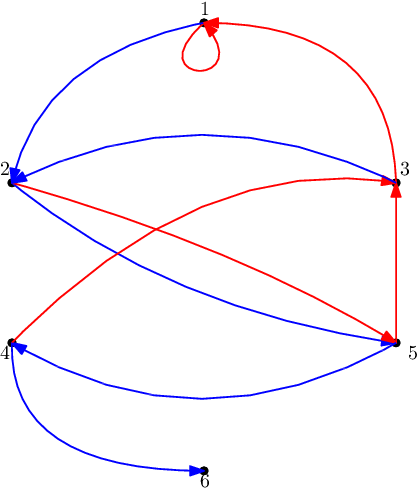
第一个样例中的图如下图所示。  前 $19$ 个询问描述了标记的移动过程。在第 $19$ 步时，标记会到达顶点 $6$。最后两个询问表示无法到达的状态。 由 ChatGPT 4.1 翻译