CF126D Fibonacci Sums

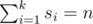
斐波那契数列定义如下： $ F_{1}=1, $ $ F_{2}=2, $ $ F_{i}=F_{i-1}+F_{i-2},i>2 $。 我们考虑一个非空集合 $ S={s_{1},s_{2},...,s_{k}} $，其中每个 $ s_i $ 都是不同的斐波那契数。我们计算该集合元素的和：  我们称集合 $ S $ 为数字 $ n $ 的一种斐波那契和分解。 很容易发现，有些数字有多种斐波那契和分解方式。例如，对于 $ 13 $，有 $ 13 $，$ 5+8 $，$ 2+3+8 $——共三种分解方式；对于 $ 16 $，有 $ 3+13 $，$ 1+2+13 $，$ 3+5+8 $，$ 1+2+5+8 $——共四种分解方式。 给定数字 $ n $，请你计算它有多少种不同的斐波那契和分解方式。

第一行包含一个整数 $ t $，表示测试用例数量（$ 1 \leq t \leq 10^{5} $）。接下来的 $ t $ 行，每行一个测试用例。 每个测试用例为一个整数 $ n $（$ 1 \leq n \leq 10^{18} $）。 请不要在 C++ 中使用 %lld 读写 64 位整数，推荐使用 cin、cout 流或 %I64d。

对于每个测试用例，输出一个整数，表示该数字的不同斐波那契和分解方式的数量，每行一个答案。

如果存在某个数仅包含在第一个分解中而不在第二个分解中，则认为两种分解不同。仅仅顺序不同的分解视为相同。 由 ChatGPT 4.1 翻译